日报标题:两个人里选一个,这票我没法儿投啊
阿罗不可能性定理(Arrow 定理)是指,如果众多的社会成员具有不同的偏好,而社会又有多种备选方案,那么在民主的制度下不可能得到令所有的人都满意的结果。
 顾归,运去英雄不自由
顾归,运去英雄不自由
尝试用比较通俗易懂的方式答一下这个问题......
假设学校里面要选优秀学生,而选择优秀学生的主要条件是看语文,数学,英语三科成绩,假设现在候选人只有小明和小红,并且根据他们的成绩单我们可以看到这样一个结果:
语文
小明>小红
数学
小明>小红
英语
小红>小明
老师一看,哎呀,小明同学在两门都比小红同学强,说明小明同学更加全面,那就选小明了!
但是这个时候,又多加了一位候选人小刚,老师们把小刚的成绩单拿过来再综合一比较,就得出了这样一个结果:
语文 小明>小红>小刚
数学 小刚>小明>小红
英语 小红>小刚>小明
老师再一看,坏了,小刚在数学和英语上都比小明强,说明小刚比小明全面;但是小红又在英语和语文上都比小刚强,说明小红比小刚全面;这样来看小红应该比小明更加全面。可是,我们一开始的结论是小明同学比小红同学更加全面啊?!这该怎么选呢?
熟悉这个场景的朋友们都知道,这就是一个经典的投票悖论:孔多塞悖论。阿罗不可能定理(Arrow's impossibility theorem)正是投票悖论的衍生。
之所以小刚的进入会对结果产生影响,就是因为在他进入后,每一个投票者(这里是语文数学英语三门学科)都产生了一个“度”的问题。在小刚进入之前,大家只知道,小明语文数学比小红好,但是好多少?小红英语比小明好,又好多少呢?现在小刚进入了,每个人(这里是每个学科)都被迫重新评价这个“度”的问题,小刚在这里成为了一把衡量“度”的尺子,使得最终出现“小明优于小红又劣于小红”的悖论。
那么有人不服气了,这样吧,我们给每个人积分,在任何一门学科上,拿第一的积三分,拿第二的积两分,拿第三的积一分,比较总积分不就行了?
这的确是一种不错的方法,在实际投票过程中也被运用,被称之为“波达投票法”。如果按照这个制度看来,小明小红小刚都是六分,大家打平了,皆大欢喜。
可是这个时候问题又来了,小刚突然又宣布退出竞选了!原因是肚子疼还是什么其他的我们先不去管他,老师们又得重新规划了,可是这个时候按照积分制,小明还是胜过了小红啊!投票结果居然与候选人的数量有关,这个便是波达投票悖论。
有的人又说了,既然如此干脆比分数吧,最后分数加在一起,谁最高谁被选上,这个方法怎么样?
老师们经过紧锣密鼓的计算,得出了这样一份表格
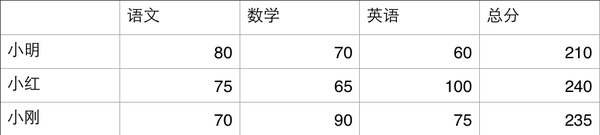
这样可以很清晰的看出答案:小红>小刚>小明,让我们为小红撒花庆祝!
别急,让我们现在把情景改一下,把小明,小红,小刚视为竞选某一职位的候选人,A,B,C 为三位投票人,每一科的成绩视为该人当选后对投票人的效用,于是这副表格就变成了这个样子:
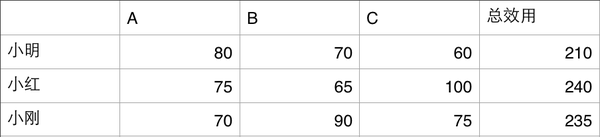
从表格中我们可以看出,选择小红是最好的结果,因为小红带来的总效用最大。
但是在事实投票中存在什么问题呢?阿罗不可能定理给我们了这样几个“完美”的投票条件:
- 自由赋序:任何人的表态都不受到限制, 即不能规定某个人对备选对象的某种表 态。
- 弱帕累托(Pareto)原则:每个人都赞成的事情,就是社会应该赞成的事情。
- 对无关备选对象的独立性:当人们对两个备选对象进行评价时, 社会根据大家对它们 的态度就能决定,不必牵涉到对其他备选对象的评价。
- 非独裁 :不能一个人说了算,而其他人的意见无足轻重。
就以我刚才举的例子来说,很显然选小红是最好的结果,选她可以给竞选人带来最大的总效用。但如果真的是三个人竞选,投票结果(按照波达投票法)将会是三个人打平。如果真的只剩下两个人(小红和小明),小红甚至会输!那么,应该怎么办呢?
一种办法是,C 说,选小红,我所获得的效用比你们两个加起来所损失的效用还要大,为了社会的最优化,就决定是小红了!
A 和 B 说:凭什么?难道不应该是一人一票吗?
C 说:不行,现在我是老大,你们得听我的!
然后就选了小红,在这个场景中,的确社会总效用达到了最大化,但是它违背了“非独裁”条件,因为投票并不是一人一票的公平竞争,而是 C 的独裁统治——如果我们排除了人际效用的可比性,而且在一个相当广的范围内对任何个人偏好排序集合都有定义,那么把个人偏好总合为社会偏好的最理想的方法,要么是强加的,要么是独裁的。阿罗不可能定理如是说。
另一种方法是,C 现在拉拢了 A,A 本来是准备选小明的,但是 C 以超过 5 的效用贿赂(或者叫结盟)A,导致 A 和 C 一起选小红,这个时候,同样可以达到总效用的最大化,但是它违背了“自由赋序”条件,使得 A 所选的并不是他真正想选的人。这样,同样也违反了“完美”投票条件的要求。
所以我们最终来看结论,阿罗不可能定理到底为什么违背我们的直觉,使得竞选人数的变化竟然会影响到我们的选择呢?就是因为每个投票人对每个竞选者选举上的效用实际上是不同的,但是在你的投票中无法直接表现出其效用的不同。在两个候选人时,你只有 YES 或者 NO 两种选择,所以没有什么直接的冲突。但是在三个即三个以上的候选人时,你对每个人被选上的效用间接的体现在你对其的排序上,无数人的效用加在一起,就出现了 A>B>C>A 这种奇怪的现象了。
这只是我个人的看法,欢迎大家的讨论和指证!