相关链接:密码学大事件!研究人员公布第一例 SHA-1 哈希碰撞实例
 刘巍然-学酥,PhD/PKE/Java/听译
刘巍然-学酥,PhD/PKE/Java/听译
多图预警,长答案预警,请在 WiFi 环境下阅读此答案。
---
写在前面
感谢知乎密码学交流群的同学 @王希 对本答案的部分地方进行了精炼,@某位老师对本答案提出了宝贵的意见。感谢安全大事件(知乎专栏)团队成员 @Murasaki 为本答案提出了改进的建议。
攻击成本问题
SHA-1 攻击成果令人惊异,据说还导致了小范围比特币的抛售…然而,事情并没有想象的那么严重。原因如下:
首先,比特币系统中一共使用了 2 个哈希函数,分别为 SHA-256、RIPEMD160。这是与 SHA-1 完全不同的哈希函数。另外,RIPEMD160 只用于交易地址的压缩,确认交易和数字签名所用的哈希函数均为 SHA-256。到现在为止学者们还没有发现 SHA-256 的漏洞,因此比特币的安全性仍然可以得到保证。
第二,正如后面答案中提到的,SHA-1 早在 2011 年就已经被建议替换。只不过因为兼容性问题和成本问题,有些对安全不太重视的厂商还在使用 SHA-1。这次的攻击结果能够促使这些厂商认真考虑替换 SHA-1 的问题,否则其产品会失去市场。对于那些对安全很重视的公司,如 Google、苹果、IBM、微软等(感谢 @唐勇 的评论,微软也是最先推荐使用 SHA-256 的公司之一),SHA-1 早已被抛弃使用了。
第三,虽然 Google 的算法是实际上可行的,但攻击成本有多少呢?论文中提到,算法的执行时间大约为 6500CPU 年和 100GPU 年。这是个什么概念呢?如果某个攻击者要使用这个算法实现攻击,它需要在 Amazon EC2 上租赁足够的 CPU 计算核与 GPU 计算核(当然了,租的越多花费时间越少)。正如论文中给出的,如果把时间成本也考虑其中,实施 SHA-1 攻击的成本虽然得到了降低,但也不少,大约需要花费 7.5W-12W 美金。这对一般攻击者来说,成本应该算比较高吧…
(注:7.5W-12W 美金的花费实际对应的是 Stevens 等人提出的另一种攻击方法,此攻击方法效率更好,但是并行处理能力相对较差。猜测新攻击方法会花费更多的费用租赁 GPU 计算核,从而实现大规模并行处理。综合考虑,个人认为两种攻击的花销接近,可能新攻击方法的花销会更大)
---
前沿
今天(2017 年 02 月 24 日)一大早,我微信的朋友圈就被刷屏了:Google 发布了哈希函数 SHA-1 的 哈希碰撞实例。同时,我的知乎上也推送了上海交通大学 LoCCS 实验室理论密码研究组发布的专栏文章:《密码学大事件!研究人员公布第一例 SHA-1 哈希碰撞实例》(专栏文章链接:知乎专栏)。
起初,我还以为 Google 团队仅仅找到了两组没有意义的数据,但 SHA-1 结果相同而已。但在晚间深入阅读了 Google 团队的安全博客,并阅读了论文《The First Collision for Full SHA-1》后,我发现我低估了 Google 所发布工作的意义。实际上,Google 发布的工作远超我之前的想象。Google 的工作基本可以宣判了 SHA-1 的死刑!
专栏文章:《密码学大事件!研究人员公布第一例 SHA-1 哈希碰撞实例》也提到一个八卦:
这个轰动性结果甚至让今年某顶级学术会议的 Deadline 为之延期!!
而这个顶级学术会议就是密码学界最为著名的会议 CRYPTO 了。在 CRYPTO 2017 官方网站上我们可以看到一个大大的红色延期标记:

一般来说,会议截稿日期延期主要是因为投稿论文数量没有达到期望值,但任意领域最顶级的会议从来不会缺少稿件。而且注意到,这次延期感觉很奇怪,只延长了 19 个小时而已。因此,能使这种重量级会议的截稿日期延期,唯一的情况就是某个轰动的结果所总结的论文将会投稿到此会议上。实际上,CRYPTO 组委会就是多给了 19 小时的时间,等待 Google 方面完成论文的撰写。由此可见,Google 这一工作对密码学理论的重要程度。这篇重量级的论文即为前面提到的《The First Collision for Full SHA-1》(原始论文:https://shattered.io/static/shattered.pdf)。相信这篇论文会被 CRYPTO 2017 录用。
本着可观科学的原则,我试图撰写一篇稍微深入的答案,为知友们深入介绍一下 Google 所做的工作,以及这个工作的意义。本答案将包括下述几个部分:
- 哈希函数简介(科普)
- SHA-1 哈希函数简介(科普)
- 《The First Collision for Full SHA-1》工作简介(科普)
- 《The First Collision for Full SHA-1》工作验证(非科普)
- 《The First Collision for Full SHA-1》工作意义(科普)
---
哈希函数简介(科普)
我相信很多知友们都听说过,或者有意无意地使用过哈希函数。知乎已经实现了全站 https,因此我们访问知乎的时候就会无意中使用哈希函数。https 的标志是浏览器地址栏的左侧会出现一个带锁的标志。以 Google 的 Chrome 浏览器为例,锁的标志大概是这样的:

如果知友们了解如何浏览 https 证书信息的话,可以通过一系列操作,最后看到这样的界面:

其中,【签名哈希算法】部分写着 SHA-256,这就是 https 所使用的哈希函数了。有趣的是,如果拖动滚动条,会发现知乎 https 证书的【指纹算法】仍然使用了 SHA-1:
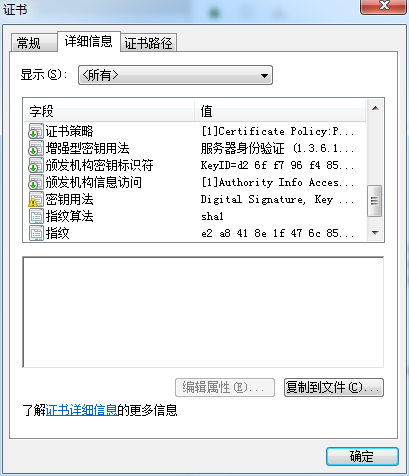
所以可能知乎所用的证书也需要更新了~
(注:实际上证书安全性的核心在于数字签名、密钥用法等,单纯的指纹算法和指纹本身对安全性没什么影响。由于数字签名使用的是 SHA-256,知乎的证书暂时没什么问题,大家还是可以放心的~)
另一个知友们可能经常看到的哈希函数使用实例在软件下载界面。下载软件时,我们经常会看到文件上传者提供了几个看似毫无意义的字符串。这几个字符串就是使用不同的哈希函数计算得到的。不过,由于互联网安全技术的不断发展,这些字符串的验证过程已经变为了后台执行,用户下载时不需要再人工比对了。例如,如果知友们于 2017 年 2 月 24 日访问著名程序语言 Java 的开发环境下载界面,则会看到这样一个警告信息:

关键地方的翻译如下:
Important planned change for MD5-signed JARs
有关 MD5- 签名 JARs 的重要变化
Starting with the April Critical Patch Update releases, planned for April 18 2017, all JRE versions will treat JARs signed with MD5 as unsigned.
计划于 2017 年 4 月 18 日发布四月的重要补丁更新,此更新后,如果 JRE 版本 JARs 文件所用的签名使用了 MD5,服务器将认为此签名无效。
正是由于著名哈希函数 MD5 已经不再安全,因此安全界才会发布这样一个计划,逐渐将 MD5 退出历史舞台。
那么,哈希函数是什么呢?简单地说,它是密码学中的一个重要的函数,一般以 表示。这个函数可以将任意一段数据(一般称这段数据为“消息”)压缩成固定长度的字符串(一般称输出的字符串为“摘要”)。哈希函数需要满足下述条件:
- 确定性:哈希函数的算法是确定性算法,算法执行过程不引入任何随机量。这意味着相同消息的哈希结果一定相同。
- 高效性:给定任意一个消息
,可以快速计算
。
- 目标抗碰撞性:给定任意一个消息
,很难找到另一个消息
,使得
.
- 广义抗碰撞性:很难找到两个消息
,使得
。
在密码学上,一般认为如果第 4 个条件不满足,那么此哈希函数就不再安全。在实际中,一般认为如果在某种程度上第 3 个条件不满足,那么此哈希函数就不再安全。当然了,如果第 3 个条件完全不满足,那么此哈希函数已经彻底不安全,应该被直接弃用。
哈希函数的(广义)抗碰撞性使得哈希函数可以用于数据的完整性验证。举例来说,某个用户上传一个文件供其他用户下载。用户在网络上公开了文件的哈希函数输出结果。下载用户完成下载后,计算下载结果的哈希函数输出结果。如果结果相等,则可以认为下载的软件就是官方发布的软件,没有遭到第三方的篡改。
哈希函数第二个常见的应用场景是密码存储。在用户进行网站登录时,如果服务器直接存储用户密码,则如果服务器被攻击者所攻击,用户的密码就会遭到泄露。最典型的事件就是 CSDN 的密码明文存储事件了。为了解决这个问题,服务器可以仅存储用户密码的哈希结果。当用户输入登录信息后,服务器端可以计算密码的哈希结果,并与存储的哈希结果进行对比,如果结果相同,则允许用户登录。由于服务器不直接存储用户密码,因此即使服务器被攻击者攻击,用户的密码也不会被泄露。这也是为什么我们在使用【找回密码】功能时,服务器直接请求输入新的密码,而不是把原始密码发送给我们。毕竟,它自己也不知道用户的密码是什么… 至于彩虹表攻击等,属于讨论范畴之外,在此不多做叙述。
(注:特别感谢 @大空格 的指正。原始答案中我写的是客户端计算哈希值后传给服务器,这是完全错误的。参考加盐密码哈希:如何正确使用 - 文章 - 伯乐在线文章中的描述:
即使浏览器端用 JavaScript 加密了,你仍然需要在服务端再次进行加密。试想有个网站在浏览器将密码经过哈希后传送到服务器,那么在认证用户的时候,网站收到哈希值和数据库中的值进行比对就可以了。这看起来比只在服务器端加密安全得多,因为至始至终没有将用户的密码明文传输,但实际上不是这样。
问题在于,从客户端来看,经过哈希的密码逻辑上成为用户真正的密码。为了通过服务器认证,用户只需要发送密码的哈希值即可。如果有坏小子获取了这个哈希值,他甚至可以在不知道用户密码的情况通过认证。更进一步,如果他用某种手段入侵了网站的数据库,那么不需要去猜解任何人的密码,就可以随意使用每个人的帐号登录。
这并不是说你不应该在浏览器端进行加密,但是如果你这么做了,一定要在服务端再次加密。
)
哈希函数第三个重要的应用是数字签名。实际上, 数字签名算法对消息的长度和格式是有要求的 ,要求数据满足一定的条件。为了解决这个问题,学者们指出可以对数据的哈希结果签名。由于哈希结果的长度是固定的,一般来说容易构造一种方法,让这个长度固定的结果进一步满足数字签名算法对数据输入的要求。而由于哈希函数的抗碰撞性,如果原始数据被篡改,那么哈希结果也会变化,同样会导致签名无法通过验证。更为重要的是,先哈希后签名的方法可以让签名变得更安全。实际上可以证明,如果先哈希,再执行 RSA 数字签名,则此算法是可证明安全的。详细信息可以参考 Katz 和 Lindell 的书籍《Introduction to Modern Cryptography》,第 13.2.3 节,OAEP。
---
SHA-1 哈希函数简介(科普)
SHA-1 是 1995 年国家标准技术局 NIST(National Institute of Standards and Technology)于 1995 年标准化的哈希函数。与前身 MD5 相比,SHA-1 的输出长度更长(MD5 输出长度为 128bit,而 SHA-1 的输出长度为 160bit),这也意味着出现哈希碰撞的概率更低。同时,SHA-1 的安全性似乎也比 MD5 更好。
这里要稍微介绍一下寻找哈希函数碰撞的难度和一般方法了。以 SHA-1 为例,其哈希结果长度为 160bit。如果 SHA-1 本身没有漏洞,而攻击者想找到一组碰撞的话,最显然的方法是选取 组不同的数据,依次计算它们的哈希结果。根据著名的抽屉原理,必然会出现一组数据,使得其哈希结果相同。此攻击方法需要调用
次 SHA-1,即计算量级大约为
。
(注:在后面的论述中,我将直接用计算量级表示调用 SHA-1 的次数)
抽屉原理很容易理解:假设有 4 个抽屉,而有 5 个苹果。我们要把这 5 个苹果放在 4 个抽屉里,那么必然至少有 2 个苹果被放进了同一个抽屉。就算前 4 个苹果均放在了不同的抽屉中,由于所有抽屉都被占满了,而第 5 个苹果也要占一个抽屉,因此这个苹果一定和前面 4 个苹果中的某个苹果放在了同一个抽屉里面。

(图片来源:课件《抽屉原理》_永恒的心_新浪博客)
虽然这么寻找碰撞一定是可行的,但计算代价太大了, 这个数量级有多夸张?对比一下,全地球沙子的数量大约为
。(参考知乎问题:地球上共有多少粒沙子? - 科普 - 知乎,我这里直接用
完成的计算,感谢 @许铖 指出了一个更确切的估计:
,看来全球沙子也还是远远不够的)
然而,我们可以通过概率方法寻找。我们放宽条件:如果降低一定的计算量,能不能有比较高的概率找到一组碰撞呢?这就是著名的生日攻击(Birthday Attack)了。
根据抽屉原理,一个屋子里必须有 366 个人(一年有 365 天,不考虑闰年)才能保证一定有 2 个人生日相同。然而,如果一个屋子里有 23 个人,则有 50%的概率 2 个人生日相同。根据概率论(感谢 @程恩琼 @韩劼群 指出原始答案中的笔误):
- 第 2 个人和第 1 个人生日不相同的概率为
;
- 第 3 个人和第 1 个人生日不相同的概率为
,和第 2 个人生日也不相同的概率为
(因为此时已经假定前 2 个人生日不同),因此和前 2 个人生日都不相同的概率为
;
- 第 4 个人和前 3 个人生日都不相同的概率为
;
- ......
- 第 23 个人和前 22 个人生日都不相同的概率为
;
- 上述事件同时发生时,23 个人生日才会各不相同。因此,23 个人中存在 2 个人生日相同的概率为:
。
寻找哈希碰撞时也可以用到这个方法。事实上可以证明,对于 SHA-1 来说,选择大约 组不同的数据并计算哈希结果,则有 50%的概率有 2 个数据的哈希结果相同。此方法的计算量级可达到
,远优于
。引入的代价是成功率变为 50%,因此计算量级的期望为
。这个量级和全球沙子的个数有点接近了,我们需要大约计算 1000 倍全球沙子个数的哈希结果后,能有约 50%的概率找到一组碰撞。
密码学上认为,如果能找到一种方法,能在计算时间小于的情况下,有超过生日攻击的概率下找到一组碰撞,则认为这个哈希函数就不安全了。
SHA-1 自提出后,学者们一直认为它是安全的,也就是说没有找到计算时间小于 的攻击方法。在 CRYPTO 2005 上(没错,和上面的 CRYPTO 2017 是一个会议),中国著名密码学家王小云教授所在的团队提出了一个一种寻找 SHA-1 碰撞的,相对快速的攻击方法(原始论文:Finding Collisions in the Full SHA-1,发表在 CRYPTO 2005 上)。此攻击方法的计算量级为
,这标志着 SHA-1 存在漏洞。这个成果使中国密码界闪耀在世界舞台!也正是因为这个研究结果,NIST 不得不着手选择新的哈希函数,因此我们现在才有了 SHA-256(知乎所用的哈希函数)、SHA-384、SHA-512 等。(感谢 @swordfeng 指出的错误,SHA-256、SHA-384、SHA-512 同属 SHA-2 系列哈希函数,原始描述将这几个名词并列放置,是不合理的)
王小云教授的开创性工作让进一步破解 SHA-1 成为可能。然而,王小云教授的方法仅可以破解 SHA-1 的广义抗碰撞性,且计算时间相对较长。因此,一段时间以内 SHA-1 还是可以使用的。学者们致力于寻找更加高效的 SHA-1 破解方法。截止 Google 的工作之前,最好的方法是 Stevens 提出的攻击方法,可以在 计算量级内找到一组哈希碰撞(原始论文:New Collision Attacks on SHA-1 Based on Optimal Joint Local-Collision Analysis,发表在与 CRYPTO 同等级的密码学顶级会议 EUROCRYPT 2013 上)。
上述方法都是纯使用 CPU 计算的方法。如果把显卡(也就是所谓的 GPU)引入破解工作,使用大规模并行处理,是否能够进一步提高效率呢?Stevens 等人又在 2016 年提出了新的攻击方法。他们指出,如果使用 GPU 并行计算,则计算量级会进一步降低到 (原始论文:Freestart Collision for Full SHA-1,发表在 EUROCRYPT 2016 上)。本次 Google 的工作也使用了类似的方法,不过由于有不可避免的困难,此次提出的攻击方法计算量级大约为
。既然计算量级反而增大了,为何这次的成果比之前的成果更加轰动呢?答案的后半部分会讲到此攻击方法的亮点。
当然了,如果你注意到的话,会发现 Stevens 正是 Google 所做工作论文的第一作者…
---
《The First Collision for Full SHA-1》工作简介(科普)
现在我们可以看看,Google 的工作(同样也是 Stevens 的工作)到底是什么?我们直接引用此工作官方网站(原始链接:SHAttered)的介绍吧:
We have broken SHA-1 in practice.
我们从应用角度破解了 SHA-1。
This industry cryptographic hash function standard is used for digital signatures and file integrity verification, and protects a wide spectrum of digital assets, including credit card transactions, electronic documents, open-source software repositories and software updates.
这一工业界应用的密码学哈希函数标准被用于数字签名、文件完整性验证中,并在多个领域保护着人们的数字财产,这些数字财产包括信用卡交易、电子文档、开源软件仓库、软件更新等。
It is now practically possible to craft two colliding PDF files and obtain a SHA-1 digital signature on the first PDF file which can also be abused as a valid signature on the second PDF file.
在实际中,我们可以构造两个 SHA-1 结果相同的 PDF 文件。这使得第二个文件 SHA-1 后的数字签名可以通过第一个文件 SHA-1 后数字签名的验证。
For example, by crafting the two colliding PDF files as two rental agreements with different rent, it is possible to trick someone to create a valid signature for a high-rent contract by having him or her sign a low-rent contract.
举例来说,可以构造两个 SHA-1 结果相同的 PDF 租赁协议文件,协议文件中标注的租金不同,但高租金文件的 SHA-1 后签名结果与低租金文件的 SHA-1 后签名结果一样。这样,可以让租赁方在低租金文件上签字,再用高租金文件替换,达到伪造租赁协议文件的目的。
Attack Proof
攻击证明
Here are two PDF files that display different content, yet have the same SHA-1 digest.
下方有两个 PDF 文件,其显示的内容不同,但 SHA-1 摘要结果相同。
从论述中可以发现,Stevens 等人成功构造了两个 PDF 文件(这是有意义、可以真正打开的文件),使得 SHA-1 结果相同!这可是比较夸张了… 我们来看看这两个文件。
- 第一个文件的下载链接为:https://shattered.it/static/shattered-1.pdf
- 第二个文件的下载链接为:https://shattered.it/static/shattered-2.pdf
第一个文件打开后是这样的:

第二个文件打开后是这样的:

惊到了好吗!不光是能打开的 PDF,PDF 的内容竟然还有意义!这让我感觉 Stevens 的工作可不是找到了一组碰撞那么简单。实际上,官方网站后续的说明也侧面说明了这一点:
File tester
文件测试
Upload any file to test if they are part of a collision attack. Rest assured that we do not store uploaded files.
请上传任意文件,来检测文件本身是否可能被这种攻击威胁。我们保证不存储您所上传的文件。
那么,Stevens 到底的工作到底如何?能做到什么效果呢?我们可能不得不阅读一下论文了。(感谢 @康尼扎罗反应 的修正建议,至于为何这样翻译,需要理解下面描述的工作原理)
---
《The First Collision for Full SHA-1》工作验证(非科普)
(本部分截图部分来自于 Stevens 等人的原始论文:https://shattered.it/static/shattered.pdf)
实际上,Stevens 等人做的工作是这样的:给定任意一个前缀数据 和后缀数据
,可以找到四组数据
,使得:
(感谢 @凌云轩雅 的指正,之前答案中 以及后续的编号有误)
于是,他们构造了一个满足 PDF 文件解码要求的文件前缀,内容为:

注意看右边的后 3 行。他们利用 PDF 文件编码方法的特性,在前缀 中插入了注释符号:$,并顽皮的接上了:“SHA-1 is dead!!!!!”,同时保证后面的部分可容下
。这样就可以保证这段恶意插入的数据不会导致 PDF 文件解码错误。而
为:

为:

为:

为:

我个人不太理解 PDF 的编码方法,猜想 在 PDF 文件中所在的位置会控制图片上方的背景颜色。之所以这么猜想,是因为 2 个图片显示结果中,只有上方背景颜色发生了变化,其它地方保持不变。而攻击方法也要求后缀
必须相同。
既然如此,我们用二进制方式打开这两个 PDF 文件看一看是否真的如此。首先打开shattered-2.pdf(注意,先是第 2 个文件),观察文件开始部分:

可以看到:
- 第 000 行至第 0B0 行是 Stevens 等人给出的前缀数据
;
- 第 0C0 行至第 0F0 行是
;
- 第 100 行至第 130 行是
;
- 后面是后缀数据
。
再打开shattered-1.pdf(现在是第 1 个文件),观察文件开始部分:

可以看到:
- 第 000 行至第 0B0 行仍然是前缀数据
;
- 第 0C0 行至第 0F0 行是
;
- 第 100 行至第 130 行是
;
- 后面是后缀数据
。
这样一来,Stevens 等人通过选择有意义的前缀数据 和后缀数据
,最终构造出满足 PDF 编码格式的文件。实际上,如果我们换一张原始图片,通过插入不同的
,也可以达到此目的。而官方网站提供的文件检测器(Filer tester)的目的就是为了检测上传的文件前缀后面是否能插入对应的 ,且使得文件仍然可以正确打开… 如果能插入,那么攻击者就可以插入不同的
,从而构造出不同的文件,但 SHA-1 结果相同。
因此,Stevens 等人的工作在特定条件下破解了 SHA-1 的抗碰撞性,即给定满足特定要求的消息 ,可以比较快速地找到另一个消息
,使得
。当然了,正如论文中所提到的, 的计算需要花费大约 6500 个 CPU 计算年和 100 个 GPU 计算年。虽然时间比较长,但利用云计算技术,已经可以在数天内完成计算了。

(图片来自上海交通大学 LoCCS 实验室理论密码研究组发布的专栏文章:《密码学大事件!研究人员公布第一例 SHA-1 哈希碰撞实例》:知乎专栏。感谢 LoCCS 实验室团队成员的指正,原始图片来自于 Google 安全博客https://security.googleblog.com/2017/02/announcing-first-sha1-collision.html)
---
《The First Collision for Full SHA-1》工作意义(科普)
Stevens 等人工作的最大意义是,可以在较短时间内寻找到有意义的两个文件,使得其 SHA-1 结果相同。虽然寻找碰撞的速度比已知的最好速度慢一些,但是输出文件有意义这一点是非常亮眼的。这对于哈希函数本身来说虽不能算是彻底的破解,但也已经很接近了。此工作基本可以宣告 SHA-1 的死刑。
不过,其实也还好。我们应该感谢一个叫做 Kerckhoffs 的研究者。这里引用 @王希 同学在问题在有限专家间评议加密算法是不是比直接公开更安全? - 网络安全 - 知乎下的回答:
(Kerckhoffs 指出)开放密码学设计则有如下四点优势:
- 公开的设计可以承受公开的钻研和分析,因此可以更加强壮。构造良好的密码学方案非常困难,更广泛地被研究可以证明其安全性。
- 公开后有更大的可能被正义黑客发现,比被敌人发现要好。
- 系统的安全取决于算法的保密性,对代码的逆向抵抗力很差。密钥不是代码的一部分,不存在这个问题。
- 公开设计使标准更容易建立。
虽然 Kerckhoffs 是在加密算法的环境下提出了公开密码学算法的概念,这个理念也被传到了哈希函数上面。自 2005 年王小云教授指出 SHA-1 的漏洞后,NIST 在 2011 年就提出反对使用 SHA-1 算法,应使用更安全的哈希函数。这给了业界大量的时间选择更好的算法,并逐渐替换 SHA-1。现在,新生成的 https 数字证书已经基本淘汰了 SHA-1。同时注意到,Stevens 等人的攻击方法还是要求消息满足一定的条件,因此 SHA-1 还没到已经彻底不安全的程度。
不过,警钟都敲成这样了,换不换?!
以上。