日报标题:想当边听边记,同时看书复习的学霸,我应该怎么做?
 Feitong Yang
Feitong Yang
如果听觉信息和视觉信息不一致,那么同时呈现两个信息,结果肯定是会互相干扰的。因为题主问的是是否能够同时记忆两段材料,说明题主想问这两段材料是否可以同时加工。所以我们就不讨论诸如『一边看新闻,一边被唠叨』这种情况了,因为我们可能直接忽略了『唠叨』的部分。其他的答案已经提到了『注意』等因素的影响,其中有人敏锐地提出了一致和不一致(congruency and incongruency)的问题,顺便提到了多通道整合(multimodal integration)。我觉得信息已经非常足了。
其他的答案说了当视觉信息和听觉信息都需要加工,而且加工还特别费事儿的时候,你基本上没法同时做两件事,所以难以同时记住两个材料。实际上,你有可能记住每个材料的一部分,但是每一个材料的记忆都会比较差。
这里,我来补充一个实验来说明:即使视觉加工和听觉加工都可以自动化(Automatic),都非常迅速的时候,如果两项信息不一致,你的加工仍然会受到严重的影响。所以,建议就是,请一心一意做好一件事情。单线程,并不可耻。
太长了;不想读
1. 人类统计学习(statistical learning)指的是人类可以自动、快速地从感知觉信息中提取出统计结果或者统计规律,比如 A 总是在 B 后面出现,C 总是在 D 上方等。
2. 这种统计学习达成的速度很快,大概 2-5 分钟之内人就能提取出简单的统计信息;而且这个学习过程通常是没有意识的,学习者并不知道自己学习到了;而且这种学习的过程通常不需要任务相关。
3. 但是即使是这样快速的学习过程,在听觉信息和视觉信息不一致、互相独立的时候,人们也无法同时学会两组信息中的统计结果,要么两方信息都会漏掉一些,要么会完全丢失其中一组信息,比如可能视觉统计结果完全学不会。
4. 不管怎么说,这是一个注意过程。人呢……还是没有办法很好地同时学习、记忆多个通道的信息的。不过,如果视听信息一致,说不定会事半功倍。
我要说的是人类 statistical learning 的研究。学计算机的朋友请停下你们的思考,这个 statistical learning 和你们的 statistical learning 基本上没有什么关系。1996 年,对幼儿语言习得感兴趣的 Saffran, Aslin 和 Newport 发现,给 8 个月大的小孩听一串连续的语音流大概 5 分钟,随后小孩能发现这个语音流中暗藏的统计结构,拉开了 statistical learning 研究的序幕。
等一下,这里有什么重要的?为什么我要在这里谈 statistical learning? 客官您不要太着急,听我娓娓道来,到最后你就知道为什么我用 statistical learning 作为一个例子来回答题主的问题了。
前面提到的语音流是这样一个序列:bi-da-ku-pa-do-ti-go-la-bu-bi-da-ku...这个序列每一个音持续的时间相同,音与音间隔时间相同,也就是说这个连续的语音流并不能简单地被分割开来——除非你敏锐地发现这个语言流暗藏的统计结构:比如 bi-da-ku 总是在一起先后出现。实际上,实验者事先就安排了这样的三元组:连续三个音,总是先后以固定顺序出现。但是不同的三元组之间先后顺序随机。这里的问题就是,我们能不能通过被动地听这样连续语音,就能抓取出三元组这样的结构呢?
结果 Saffran 他们发现,8 个月大的婴儿在 5 分钟之内就可以抓取出这样的三元组信息。在 5 分钟的播放之后,他们面对两个不同的三元组,比如 bi-da-ku 和 bi-pa-do,8 个月大的婴儿能够分辨出 bi-da-ku 是 TA 之前听到过的。这个实验很有意思,原因是如果你考虑你从小学说话的时候,你听到的语句不是一个词一个词单独出现的,而是一句话一句话出现的。在单词之间可能并没有语流上的停留,但是你从来不会把一句
我今天好高兴啊
听成
我今 - 天好 - 高 - 兴啊
而是
我 - 今天 - 好 - 高兴 - 啊
你在学习语言单词的过程中,可能就是无意间,因为不同的字相邻出现的概率更大,所以你就学会了由这两个字组成的词,由此你学会了分割一个句子,并且理解句子的含义。
当然,这样的统计学习的能力,不仅仅发生在听觉系统,视觉系统同样存在。从 Fiser & Aslin 2001, 到 Fiser & Aslin, 2002, Kirkham, Slemmer, Johnson, 2002, 到 Turk-Browne, Junge, Scholl 2005, Turk-Browne, Isola, Scholl, Treat, 2008, 到 Kim, Seitz, Feenstra, Shams, 2009 及以后(如果你并不想了解参考文献,请直接看结论),实验已经证明统计学习的能力在视觉和听觉的通道都存在,而且这种统计学习能力极其迅速且自动。观察者大概只需要被动地暴露在一个信息流(语音流或者序列视觉呈现)大概 2-5 分钟,就可以学会其中的统计结构。观察者通常没有意识到自己学会了这样的统计结果,而且观察者在学习过程中完全在做一个和学习无关的任务(比如就坐着听,或者看一系列的形状中有没有特定的目标形状)。
这样一个迅速、自动的学习过程,理论上不怎么需要注意来引导加工的,所以,题主就可以问:同时呈现一个视觉序列,和一个听觉序列,每一个序列有自己的简单的统计结构,观察者能不能同时学习到这两个独立的统计结果?因为统计学习如此迅速自动,似乎有很大的可能两个统计结果都能学会!
答案是否定的。
即使这样一个快速自动的学习过程,在听觉信息和视觉信息的统计结果独立、无关的时候,人们对于两个信息中的统计结构的学习就差了很多,正确率显著下降,甚至降到了随机水平。Robinson & Sloutsky (2013)就做了这样一个实验,他们的刺激如下图,你可以发现所谓的统计结构都是一个个的三元组:或者三个音素、或者三个形状。在三元组内,元素总是以固定顺序出现,我们称为转换概率(transitional probability)为 1;在不同的三元组之间,转换概率均匀分布。
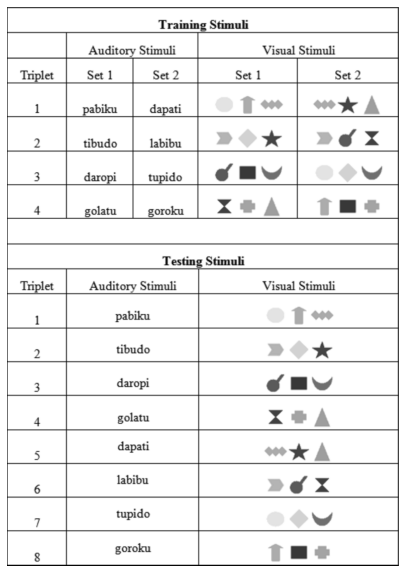
(Robinson & Sloutsky, 2013; Figure 2)
他们的主要结果是:如果视觉刺激和听觉刺激单独呈现,或者他们相关时,观察者可以同时学会视觉结构和听觉结构。但是当两个刺激随机交错,互相独立时,正确率就较低了很多。而且视觉结构基本上就没有学会(这里有意思的是,他们发现这种不一致的情境下,听觉学习并不太受影响,视觉学习受到了严重的影响,所以他们说听觉主导了视觉。具体细节可以参看 paper)
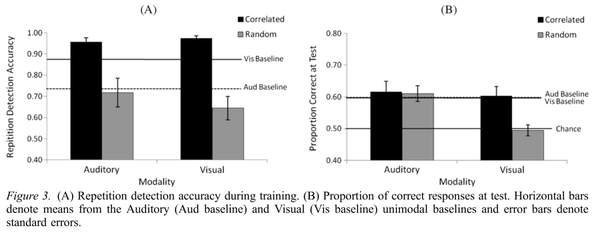
这里就是用这个简单的实验说明一下:即使是快速自动的学习能力,也会在听觉和视觉信息不一致的时候收到严重影响,结果你要不学不了视觉信息,要不学不了听觉信息,要不两个信息都学得不好。但是,如果两个信息一致的情况下,说不定你会事半功倍。
Reference
Saffran, J. R., Aslin, R. N., & Newport, E. L. (1996). Statistical learning by 8-month-old infants. Science, 274(5294), 1926-1928.
Robinson, C. W., & Sloutsky, V. M. (2013). When audition dominates vision: Evidence from cross-modal statistical learning. Experimental psychology, 60(2), 113.
Fiser, J., & Aslin, R. N. (2001). Unsupervised statistical learning of higher-order spatial structures from visual scenes. Psychological science, 12(6), 499-504.
Fiser, J., & Aslin, R. N. (2002). Statistical learning of higher-order temporal structure from visual shape sequences. Journal of Experimental Psychology: Learning, Memory, and Cognition, 28(3), 458.
Kirkham, N. Z., Slemmer, J. A., & Johnson, S. P. (2002). Visual statistical learning in infancy: Evidence for a domain general learning mechanism.Cognition, 83(2), B35-B42.
Turk-Browne, N. B., Jungé, J. A., & Scholl, B. J. (2005). The automaticity of visual statistical learning. Journal of Experimental Psychology: General, 134(4), 552.
Turk-Browne, N. B., Isola, P. J., Scholl, B. J., & Treat, T. A. (2008). Multidimensional visual statistical learning. Journal of Experimental Psychology: Learning, Memory, and Cognition, 34(2), 399.
Kim, R., Seitz, A., Feenstra, H., & Shams, L. (2009). Testing assumptions of statistical learning: is it long-term and implicit?. Neuroscience letters, 461(2), 145-149.