 匡世珉,闭关修炼
匡世珉,闭关修炼
(多图,流量党慎入!)
我来讲一个四年前的故事。
初三的某节数学课上,我突发奇想:
在圆周上的 n 个点两两连线,最多可以把圆分成几份?
(不要问我为什么会突然想到这个问题……)
于是我就拿出纸和笔开始画起来——

一个点显然连不了任何直线,所以整个圆还是 1 份;
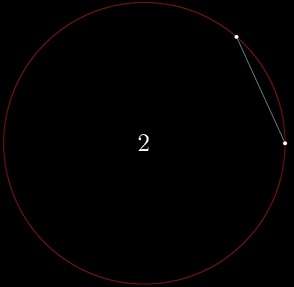
两个点之间可以连一条线,这样圆就被分成了 2 份;
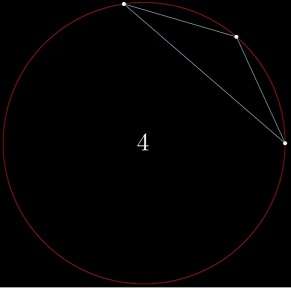
三个点可以连成一个三角形,圆被分成了 4 份;
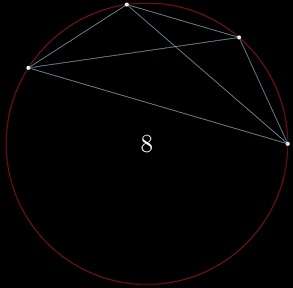
四个点两两相连把圆分成了 8 份。
啊,这个规律似乎已经很明显了,1、2、4、8,那么下一个肯定是 16 嘛!
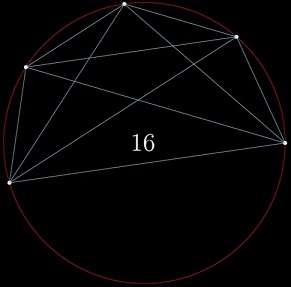
果不其然,五个点两两连线,圆被分成了 16 份。
于是,我觉得自己已经解决了这个问题,直到……我决定再加一个点。
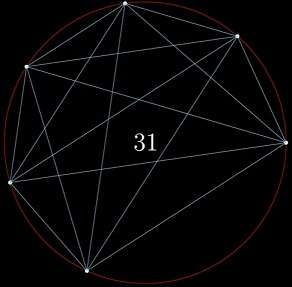
为什么是 31 份???
我又数了一遍,还是 31 份,并且在圆内也没有出现三线共点的情况……
这是什么情况???

于是我又加了一个点:
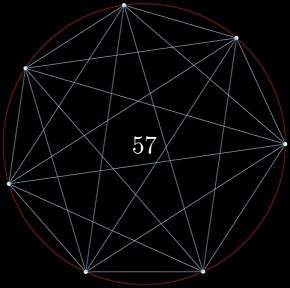
七个点,57 份。
啊,这下跟 2 的幂彻底没有关系了。
那规律到底是啥呢?
在与几个朋友一起讨论了数个小时之后,我们找到了答案。
为了分析这个问题,我们不妨先好好审视一下其中的一条直线,看看它是怎样把圆分割开的:
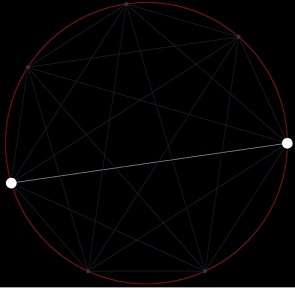
以上图中突出显示的这条线为例,假设它是从左往右画上去的,我们重现一下画图的过程:
从左端点开始,慢慢向右画,每当它碰到一根其他的直线段时,它就把某一块区域彻底地分成了两份,于是总份数就多了一;而当它最后抵达圆周右侧上的点时,总份数又多了一。
也就是说,圆内部的每一个交点都使得总份数增加了一;除此之外,每一根直线段最后抵达圆周时,总份数也增加了一。
所以,总份数应该是 1 +『圆内部的交点数量』+『直线段的数量』。
为什么会有一个 1?因为圆本身最开始就有一份啊。
我们先来求直线段的数量——这个很简单,由于 n 个点中每两个点之间都可以连一条直线段,所以这就相当于是在求『n 个点中选 2 个点有几种选法』,也就是 .
那圆内部的交点数量怎么求呢?
注意,虽然每个交点都是由两条直线段相交而成的,但我们并不能把这个问题简化为『m 条直线段中选 2 条直线段有几种选法』,因为并不是每两条直线段都相交的。
那怎么办?
(再往下继续看之前,大家可以自己先想一想=w=)
(提示:对角线)
啥意思?
再放一张图来提示一下:
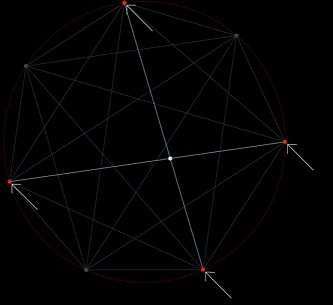
好了我要说答案了:
我们可以把圆内部的每个交点看成是某个圆内接四边形的对角线交点,于是在 n 个点中,任意四个点的组合都对应了圆内部的某个交点。
所以求圆内部的交点数相当于是求『n 个点中选 4 个点有几种选法』,也就是 。
于是我们最终的公式是:
啊。问题解决了……
吗?
等等,我还没回答题主的问题呢。所以说这有啥『巧合』?
没什么巧合。至少当我在初三那年找到了上述解答之后,我觉得没什么巧合,问题已经解决了……
直到半个月前我看到了这个视频:A Curious Pattern Indeed
我真想狠狠扇自己的脸!我当年竟然没有多问一句:
为什么当 n 比较小的时候,份数恰好是 2 的幂?
而且,当 n 等于 10 时:
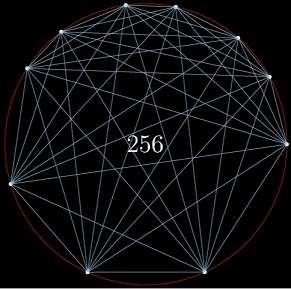
256 份!又是 2 的幂!
为什么??真的只是巧了吗???
我非常赞同 @郁林成森在回答中所说的:
数学中所有美的巧合都有其更深刻的原因,绝不仅仅是巧合。
所以说这到底是为什么呢?
原因跟这个东西有关:

这不就是杨辉(帕斯卡)三角形么?除了最左与最右的 1 以外,每个数都是由其左上与右上的两个数相加得到的。这我早就知道了,可是跟这题有啥关系?
啊,说得很对,杨辉三角形的构造方法确实很简单,不过……让我们算一算每一行的和:

咦!为什么刚好是 2 的幂呢?
我们可以换一个角度来看杨辉三角形的构造方法:
每一个数被复制了两份,分别加进了左下角与右下角的两个数中。
所以下一行的和自然是上一行的两倍,而由于第一行的和是 1,所以每一行的和就都是 2 的幂啦!
哦原来是这样,好有道理!不过这跟分圆有啥关系啊?
啊,这是因为,杨辉三角形还有另外一种形式:

我去!这是为啥??
啊,这其实只需要证明 就好了:
如果我们要从 n 个苹果里选 k 个苹果,那么我们有 种选法;而假设 n 个苹果中有一个是坏苹果,那么这
种选法中,选到坏苹果的有
种(要在除去坏苹果的 n-1 个苹果中选 k-1 个),没选到坏苹果的有
种(要在除去坏苹果的 n-1 个苹果中选 k 个),所以
。
啊,当我把杨辉三角形写成这种形式之后,之前分圆的公式与 2 的幂的关系就很紧密了!
由于 ,所以实际上 n 个点情形的公式就是杨辉三角形中第 n 行第 0、2、4 列的和。(注意,我们是从 0 开始数的!)
比如,当 n=5 时,份数就是第 5 行第 0、2、4 列的和:

写成之前的形式就是这样:

由于每个数都是左上和右上两个数的和,所以这三个数的和其实就是上一行的和:

而我们之前已经说过,杨辉三角形每一行的和都是 2 的幂,所以当 n=5 时,份数是 2 的幂。
当 n 更小的时候,情况类似。
而当 n=6 的时候,问题来了:

写成原形式:

而此时,它们的和就不是上一行的和了:

少了最右边的一。
这就是为什么 n=6 时,结果是 31 份。
而当 n=10 时:

这三个数刚好是上一行的一半:

而 2 的幂的一半也是 2 的幂,所以 n=10 时,份数 256 就是 2 的幂啦。
这就解释了我们之前的『巧合』=w=
顺带说一句,杨辉三角形其实水很深,我们甚至可以在杨辉三角形中找到斐波那契数列,不过这里我就不细说了。
这篇回答的配图来自于 Circle Division Solution,不过我初三时的推导方法要比视频中的简洁得多。视频里用了欧拉公式,麻烦了不少,不过也挺有趣的。
那么就这样=w=