日报标题:「越努力,就越幸运」,这个道理可以用数学证明
 王平民ing,一只特立独行的土木狗!港航工程设计小菜鸟
王平民ing,一只特立独行的土木狗!港航工程设计小菜鸟
概率论数理统计学上有这样的规律:总体样本越大,概率越接近真实值(实力);总体样本越小,随机性影响越高。高票建模的回答(请参看 @ssynhtn Huang) 体现的就是这个思想,即实力越强,总体样本越大越对自己有利;实力越弱,总体样本越小越对自己有利。(建模结果请参看 @王赟 Maigo )
(知乎日报注:如需参看其他回答请点击文末「查看知乎讨论」)
其实题主的这个问题就是高等数学概率论与数理统计课程中的大数定律。什么是大数定律?
大数定律(law of large numbers),是一种描述当试验次数很大时所呈现的概率性质的定律。但是注意到,大数定律并不是经验规律,而是在一些附加条件上经严格证明了的定理,它是一种自然规律因而通常不叫定理而是大数“定律”。而我们说的大数定理通常是经数学家证明并以数学家名字命名的大数定理,如伯努利大数定理。
在随机事件的大量重复出现中,往往呈现几乎必然的规律,这个规律就是大数定律。通俗地说,这个定理就是,在试验不变的条件下,重复试验多次,随机事件的频率近似于它的概率。比如,我们向上抛一枚硬币,硬币落下后哪一面朝上本来是偶然的,但当我们上抛硬币的次数足够多后,达到上万次甚至几十万几百万次以后,我们就会发现,硬币每一面向上的次数约占总次数的二分之一。偶然中包含着某种必然。(以上内容来自百度百科)
所以题主为什么觉得 10/100 比 1/10 困难?就是因为 1/10 偶然性、随机性较大,实力不足者更能利用这种随机性和偶然性(其实就是运气)获得成功,也就是对实力强者很有不利;而 10/100 却更能体现出自身实力来,随机性和偶然性影响相对较小,实力不足者自我实现更难,而对实力强者有利。当然,这个解释的前提是人群的能力表现是按照正态曲线来分布的,并且这个分布也是符合自然规律的。
总结:题主关于“该理解为同样 10% 的录取率,还是理解为“打败 9 人”比“打败“ 90 人”容易?”这个理解我个人认为是片面的。假如把 100 人分为 10 組,每组选出胜出的 1 人,虽然最终计算概率是 10/100,但是实际胜出的人只需要打败同组 9 人即可。所以,讨论 10/100 难还是 1/10 容易的问题,还必须设定前提条件:实力问题和分配原则(或者说方式,前面说的选出 10/100,是按照 100 人同时比赛方式还是按照分 10 組每组选 1 人的方式),脱离了这两个条件的讨论是没有意义的。
后记:这里所说的随机性和偶然性,我认为就是日常生活中说的运气,幸运。总结起来,获得成功的因素有两个:实力和运气。
详细地解释一下这个答案,是这样的:
总说明:
- 以下补充未在额外说明的情况下均默认人群能力是在符合正态分布模型的前提下讨论,即认为人群能力分布中间者居多,能力较强和较弱者分布较少的中间大,两边小的分布。
- 在用数学模型讨论时,所有数据均用客观性评价,即仅从数学的角度讨论,不讨论其他因素(例如家庭关系、人脉等等)的样本结果的影响。
1. 为了直观说明 1/10 和 10/100 的录取难度,现建立这样一个模型:
人群能力均匀分布在(0,1)之内并且相互独立,以 0.01 的长度计算,即能力在 0.00, 0.01, 0.02……0.98, 0.99, 1.00(用 x 表示)的 100 种情况下在每种情况下被成功录取的概率,并绘制出曲线。
对于 1/10 招录比例来说,成功录取要打败其他 9 个人,而每次成功概率为 x,那么成功概率为:P=
对于 10/100 来说,成功录取要至少打败其他 90 个人,即录取可能性为打败 90 人,91 人,92 人,93 人……98 人,99 人,求和即可得到。而每次成功概率为 x,那么成功概率为:P=
绘制出两种情况的概率分布曲线为:
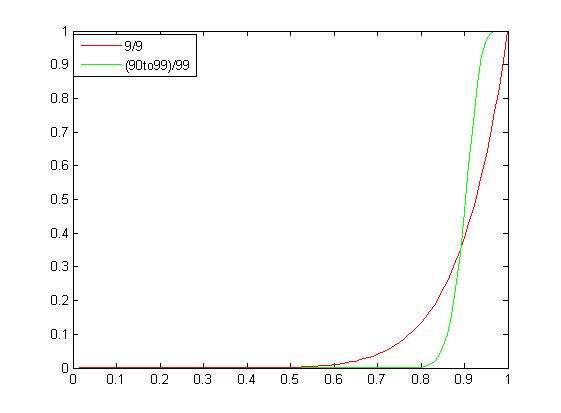
由曲线可以看出,在相同的概率下,1/10 对能力弱者和中等能力有利,10/100 对能力超强者有利。
2.为了更直观的说明大数定理,用 MATLAB 做了一个图.
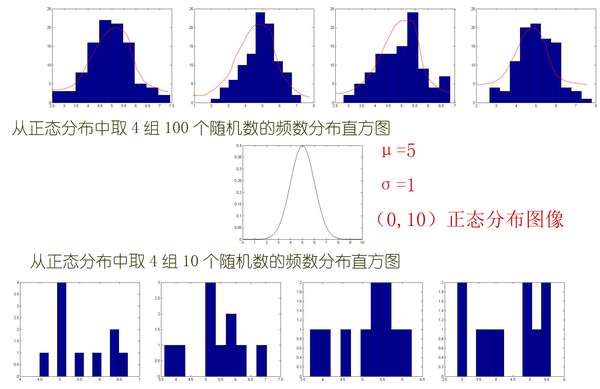
从图像上看:同一个样本容量分布,取不同数量的样本数量研究得到结论是不同的,取 10 个样本时,随机性的影响特别大,几乎是乱序的,而取 100 个样本时,虽然与随机性影响,但是样本分布基本满足正态分布中间大,两边小的特点,因此,取无穷个样本时,样本分布完全满足正态分布形态。这里说一下中心极限定理,被认为是(非正式地)概率论中的首席定理,设从均值为μ、方差为σ2;(有限)的任意一个总体中抽取样本量为 n 的样本,当 n 充分大时,样本均值的抽样分布近似服从均值为μ、方差为 σ2/n 的正态分布。
3. 对人群能力分布建模
取两组数据,两组数据能力最弱者为 0,能力最强者为 1,样本均值均为 0.5
第一组样本分布在(0,1)之间 10 个样本,相邻样本为 0.1 个长度即样本为
0.0, 0.1, 0.2……0.9, 1.0
MATLAB 计算标准差 σ = 0.3317,
按照正态分布表示为 N(0.5, 0.33172)在区间(0,1)分布
第二组样本分布在(0,1)之间 100 个样本,相邻样本为 0.01 个长度,即样本为
0.00, 0.01, 0.02……0.99, 1.00
MATLAB 计算标准差 σ = 0.2930
按照正态分布表示为 N(0.5, 0.29302)在区间(0,1)分布
用 MATLAB 绘制 N(0.5, 0.33172)和 N(0.5, 0.29302)在区间(0,1)的正态分布图像为下图所示:
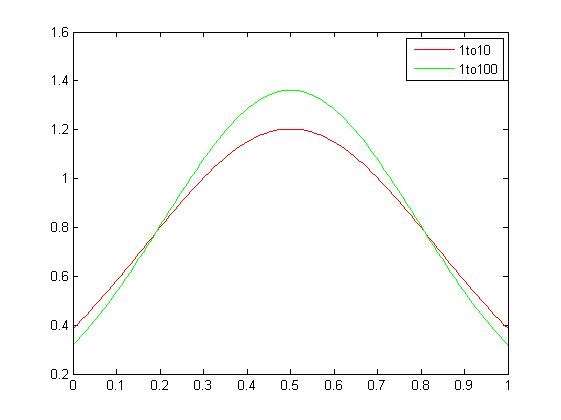
概率密度函数为正态分布的期望值 μ 决定了其位置,其标准差 σ 决定了分布的幅度。从图像和计算数据可知,10 个样本数据分布更加矮胖,即更加离散,随机性的影响相对于 100 个数据样本更大。这里说的随机性影响更大的说从无穷样本库:能力最弱者为 0,能力最强者为 1,样本均值均为 0.5 的区间(0,1)之内无穷个数据取出 10 个数据样本随机性大于取出 100 个样本的随机性,取出 10 个数据相邻数据间隔长度更大,不均匀可能性更大。举例一项考试,招录比例为 1/10 和 10/100,那么 1/10 更有可能取到 1 个能力超强,其他 9 人能力超弱的组合。
4. 随机性的影响有三层含义。
a. 从样本总体容量大小的角度看。
结合 1 和 2 以及大数定理,样本容量越小,获取的样本表现标准差越大,随机性越大。反之样本容量越大,样本数据离散程度越小,随机性越被弱化,样本越服从样本的总体规律表现,这里的随机性可以理解为样本之间偏差大小,无序性和无规律性的程度。
b. 从样本个体之间能力表现的角度看。
样本个体之间的能力越接近或者说偏离程度和间隔长度越小,随机性的个体的成影响越大,而这种影响往往是致命的。为了更好的说明,我举个例子:
乒乓球是中国国球,在我国长盛不衰,大多冠军被中国拿走,乒联于是做了一系列改革,像 11 分制,小球换大球,无遮挡发球等。以前是 22 分制,改革后为 11 分制 ,局数减少,增加了比赛的偶然性和随机性,其实这些改变都是针对中国选手,增加了比赛悬念,提高了比赛观赏度。但这主要是想减少中国对乒乓球的垄断。同样情况的还有针对中国的羽毛球联赛规则改革。
c. 从样本个体本身能力表现的角度看。
当样本个体能力确定时,建模时常常忽略个体能力的表现,并不是个体的能力表现好,个体的结果表现就一定符合能力值,比如高考超长发挥,正常发挥,失常发挥,这也是随机性的一种表现形式这里的随机性就是幸运值,建模很难体现出来。比如有不少高考状元坦言,自己平时模拟考不都是年级第一,具体例子可以百度:浙江高考理科状元李乐平时班里排十几名,2014 年四川高考理科状元封凡从未拿过年级第一等等。
5. 总结分析:
a. 从现实实际情况来看,1/10 和 10/100 这个比例常常是达不到规定招录比率的。例如以国考为例中新网北京 11 月 30 日电 29 日下午 17 时,2016 年国考公共科目笔试正式落幕。据统计,本次考试共有 139.5 万人通过招录机关资格审查,近 93 万人实际参加考试,超 46 万人“弃考”。所以实际比例是趋向改变的。
b. 建议能利用其它因素(例如家庭关系、人脉等等)的参赛者选择参赛人数少的考试。比如 10/100 情况下,你考 20 名,刷去 10 人难度大于而 1/10 时,你考第 5,刷去 4 人的操作难度。
c. 建议我们大多数人参加录取人数多的比赛。对于我们大多数人来说,参加 10/100 的比赛,自己可以控制的空间比 1/10 大,也就是公平性越大。
d. 对于随机性的影响,随机性的具体表现可以理解为幸运值。但是随机性这种事,掌握在上帝手中,对于幸运值的来说,我想:
越努力,越幸运;
而以我们大多数人努力的程度,根本还没到拼智商的地步;
同样的以我们大多数人努力的程度,远远没有到拼幸运的地步。