日报标题:马桶里的水溅到屁股上这事儿,用几篇物理实验论文分析一下
 梁昊,物院本科生
梁昊,物院本科生
还是先把结论列出来吧:
一坨东西掉到水里,在不同的参数下,激起的水花有三种不同的形态。而这三种形态在我们大便的时候都有可能遇到。
有不够充分的证据表明,第二种形态下,水花溅起的最大高度正比于物体自由落体的释放高度,而这个比例系数自然和其余参数相关
明确物理问题
我们考虑一个半径为 D 的固体球以速度 v 落入水中(为什么只是球?我们做物理的可是只研究真空中的球形鸡的哼),这个球被认为是从高度 h 处静止释放自由落体,自然有
作为与流体有关的问题,我们自然需要考虑这些参数: 即水的密度、黏度、表面张力系数。
拿到这五个参数之后我们可以得到两个无量纲数 :
,反映粘滞力的影响,常被用来度量湍流的参量
,反映动能与表面张力能之比
除此之外,作为固体与流体相互作用的问题,我们还有一个无量纲参数,即球与水的接触角 ,反映其是疏水性材料还是亲水性材料。
根据无量纲处理的一般思路,由这三个无量纲数就可以唯一确定我们需要的结果:溅出水的最大高度与球自由落体的起始高度之比。
物理图像
(这部分的图片摘自 Kubota Y, Mochizuki O. Splash formation by a spherical body plunging into water[J]. Journal of visualization, 2009, 12(4): 339-346.)
根据这些无量纲数处于不同的范围,整个物理过程表现出不同的特性。(这部分的讨论中球皆为表面进行了抛光处理的腈纶球,接触角为定值而不改变)
当 Re 和 We 较小时,黏滞力和表面张力的影响较强,一个典型的过程如下图

(图中的时间以 D/v 为一个单位,下同)
可以看出,当球进入水中后,较强的表面张力在球后方维持了一个较稳定的空腔。当球继续下沉,空腔被两端涌入的水替代。涌入的水填满空腔之后相互间发生碰撞,向正上方激发出一个锥状的水花,没有出现水花四溅的情景。
被这类水花直接命中屁眼的情况我相信大家是有体会的。
随着 Re 和 We 的增大,物理过程发生了显著的变化,两个典型的过程如下图

a, b 两组图是同一参数区域下两个不同参数的情景。
仔细观察 T=0.12 的两幅图,注意球的下部,可以看到有一层水膜(film)沿着球的表面往上爬,并在最前沿形成波浪状花纹(fingers);
在 T=0.25 时,a 图中的水膜依旧在往上爬,而 b 图中的水膜已经有溅出去的迹象。水膜是否溅出去取决于离心力与吸附力的强弱,而水膜上升的速度一般在球体下降速度的 2~5 倍间(James Oliver, Water entry and related problems, PhD Thesis, Oxford University (2002)),因此球体下降的越快,水膜越早发生溅出。注意水膜前沿的波浪状花纹,花纹数目是可以从理论上计算的,有
(Allen. R. F., The role of surface tension in splashing., Journal of Colloid and Interface Science, 51 (1975), 350-351.);
在 T=0.75 时,水膜的最前段在顶部汇合,发生碰撞而向外溅出。很明显的,水膜前段的波浪状花纹越多,则碰撞后激发出的水滴数越多;
T=1.14 时,随后跟着上来的水发生较剧烈的碰撞,形成较大的水花。
在这个情形下,我们发现无法形成气体空腔。
随着参数的继续变化,落水过程又呈现出了新的面貌,如下图
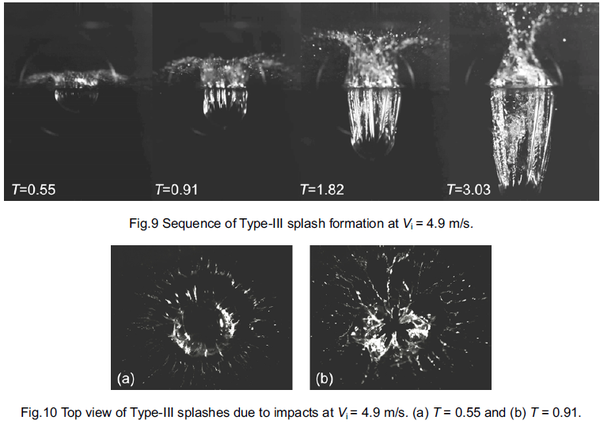
在 T=0.55 时我们可以观察到溅出的水花,随后球的迅速下降会导致表面不规则的空气空泡出现。随着两边液体的迅速靠拢碰撞,一个相当大的、破碎的水花将被激发出来。
一篇发表在 Nature Physics 上的文章(Duez C, Ybert C, Clanet C, et al. Making a splash with water repellency[J]. Nature Physics, 2007, 3(3): 180-183.)指出,对于与液体接触角小于 的亲水性固体,第二种水花和第三种水花出现的分界点在
处(即当这个参数大于 0.1 时会变成第三种水花),以常温下的水做计算,这个临界速度大致在
间。
这个情景我相信上过农村里的那种厕所的小伙伴们深有体会(坑口到底部起码 0.5m 以上)。
关于题主的问题
题主想问的是,在其他参量给定的情况下,溅出水的最大高度和球的入射速度间有什么关系?很遗憾的是,我并没有找到什么对于溅出水最大高度感兴趣的文章(当然,找到了不少写跳水怎么压水花的文章,但这些做体育物理的人写的文章就只知道一个劲的用电脑跑模拟,也不分析分析结果)唯一的一篇文章是上一个部分的图源,他研究了在第二类水花的情形下,仅改变入射速度,溅出水的最大高度。
他的结果很简单:
溅出水的最大高度和球自由落体的释放高度之比为几乎常数,且小于 1。
但是,这个结论不能简单的推广到一般。
问题的结果与两个无量纲参数 Re, We 直接相关(让我们暂且略去接触角),这篇文章等于是在这个二维平面上画了一条曲线
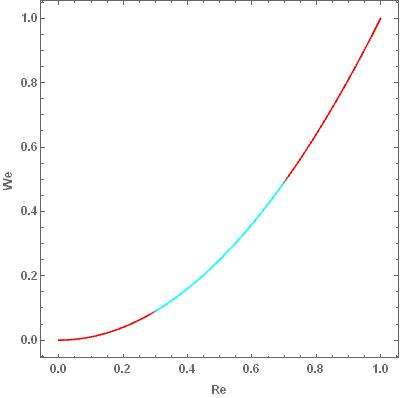
并且在中间那段天蓝色的曲线段上得到了一个结论。
那么,当我们换了球,换了不同的液体,再考虑同样一个问题时,等于是在这个二维平面上新画了一条曲线。
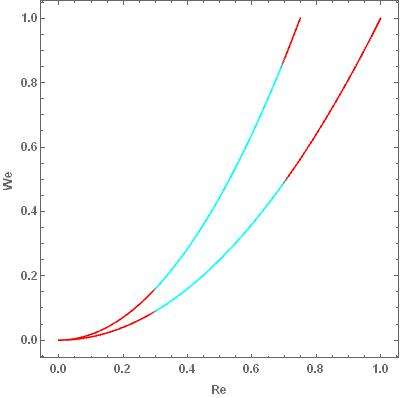
原来那段线上的结论能不能推广过来呢?
我们不知道。(摊手
当然我们可以猜测,但是对不对需要实验来检验。
其他:
题主的问题我就只能回答到这个层面上了,我再说点其他东西吧
要防止溅水的话最简单有效的办法题主也说了——垫一张纸。
当然我们还可以开点别的脑洞,比如说这篇论文
Bergeron, V., Bonn, D., Martin, J.-Y., Vovelle, L., Controlling droplet deposition with polymer additives, Nature 405 772-775 (2000)
通过向水中加入少量高分子聚合物来改变水的性质以减小水花。
还是上面说的那篇 Nature Physics 上的文章,考虑了接触角变化后激发的水花。
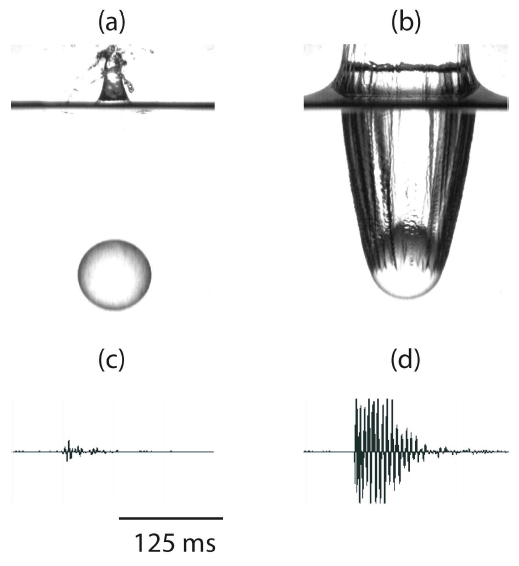
左右两副图中的球,除了左边与水的接触角是 15 度(亲水)而右边与水的接触角是 100 度(疏水)外,几乎没有任何区别,但是它们激发出的水花和空气泡却有天差地别。
由此我们可以给出一个新的建议:改变饮食结构,使得拉出的翔具有很好的亲水性。
