日报标题:光线都被引力扯弯了,天体之间的位置该怎么测量?
 狐狸先生,研究天文学的狐狸
狐狸先生,研究天文学的狐狸
简单的说,引力透镜效应确实会使得光线弯曲,改变远处天体在天球上的位置。大多数时候,这种位置改变比较小,对研究具体问题影响不大。对于特别的问题,这个效应很重要,我们可以通过对引力透镜建模来部分的解决这个问题。
关于引力透镜背景,可以看我的这个回答如何分辨宇宙中的光线是否被引力弯曲? - 狐狸先生的回答
1. 宇宙中的物质分布其实很稀疏,对于近处的天体,大多数时候光线并不会经过大质量天体。比如,测量银河系内部的恒星位置的时候,一般不需要顾及引力透镜效应。
2.宇宙深处的天体确实会受到这种效应的影响。但是即使是宇宙最深处的星系,位置也很难多次被改变。而且往往改变幅度并不大。研究大多数问题,不需要考虑这种偏折。事实上,由于引力透镜效应造成的亮度变化可能对研究的影响更大一些。
3. 对部分研究者来说,这种偏折确实很重要。这种情况属于“强引力透镜”研究。比如下图就是一个强引力透镜系统。最左边的图片是哈勃空间望远镜拍摄的,方框中的星系是一个椭圆星系,如果放大这个星系的图像,你会发现它周围有另一个星系的图像(中间),椭圆星系引力场扭曲了这个远处星系的光线,使得这个星系的图像变成了中间环状的样子(被称作爱因斯坦环)。中间高分辨率图像是射电望远镜阵列 ALMA 拍摄的,在 ALMA 的波段,椭圆星系是看不见的。
在这个实例里,远处的星系扭曲的很厉害,位置不但改变了,而且变出了两个像。为了得到这个星系原本的位置,就需要建立整个透镜系统(包含前景的星系,背景的星系)的模型。一般模型中包含若干参数,通过调节这些参数,研究者可以生成不同的模拟图像。经过和观测图像对比后,最好还原观测图像的模型被认为是最佳拟合模型。基于这个最佳模型,研究者就可以还原远处星系原来的样子和位置。经过研究,这个星系真实的位置,和前景的椭圆星系几乎一样,最初的样子就是最右边的图像。
当然,这种还原的准确度是依赖于观测的质量,以及模型建立的准确度的。这种建模研究仍然是天体物理中的一个热门话题。研究者仍然在开发更好的建模方法。

Image via ALMA (NRAO/ESO/NAOJ)/Y. Tamura (The University of Tokyo)/Mark Swinbank (Durham University).
 周恩平
周恩平
@狐狸先生 的回答在实用性的层面上已经足够好了,不过因为我自己很久以前曾经思考过广相里类似的问题所以回答一下,首先引用一段 Carroll 在 Spacetime and Geometry 里 104 页的一段话,这段话其实已经回答了楼主想要问的问题了:
………we simply must learn to live with the fact that two vectors can only be compared in a natural way if they are elements of the same tangent space. For example, two particles passing by each other have a well-defined relative velocity, which cannot be greater than the speed of light. But two particles at different points on a curved manifold do not have any well-defined notion of relative velocity -- the concept simply makes no sense……
。深刻理解这段话的话,楼主的问题就不再是问题,而我接下来要谈的东西基本由此展开
首先把这段话总结成便于理解的中文并推广一下:在广义相对论里,只有当两个物体邻近的时候才谈得上测量(比如测量相对速度)的概念,当两个物体在时空中分离开时,测量的定义是病态的,或者说根本不存在测量这个概念。因为如果我们非要比较两个在时空上分离的两个客体的相对性质,就牵扯到弯曲时空里张量的平移,而弯曲时空里张量的平移却是根据你平移的路径相关的,因而把通过某种方式把两个分离的张量平移到一起再做运算的结果,是依赖于你如何平移的。
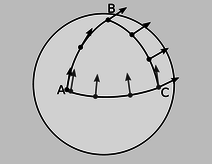
(一个烂大街的例子,在球面上想要把 B 点那个矢量平移到 C 去,可以选择 B->A->C 这条路径也可以选择直接走 B->C 的右边那条路径,而最后平移到 C 处后的结果却大相径庭。)
具体到实际来说,对于那些遥远天体(那些已经不在我们地球的邻域因而跟我们之间不能用一个接近平直的时空来联系的天体)我们所做的所有的通过“观测”而推出的“测量”,也就是如 @白书旭 所描述的那些方法,实际上都不是严格的(因为这些测距方法大都与欧氏几何相关联,比如凡是通过绝对星等与视星等来测距的方法其实都隐含了球体表面积正比于半径平方这样一个欧氏几何结论),这些“测量”的结果取决于我们是靠什么“测量”以及想通过什么“测量”,还有就是我们观测的信息(这里就是光子)在从遥远天体到地球中间经历了什么样的弯曲时空。由于脱离了平直邻域近似之后测量定义的崩塌,在宇宙学尺度上想要确定空间位置,哪怕对于同一个源、同一个观测来推出的东西也会让你大吃一惊:
我们假设有一盏巨大的灯泡被运到了距离地球很远的一个地方,一个固定功率的灯泡离观测者越远就会变得越暗,距离拉远 k 倍亮度就会减小 k^2 倍,那么我们依据这个可以根据灯泡的可视亮度来推算一个距离,这个叫光度距离(Luminosity distance)
另外呢,这个灯泡非常巨大(比如有一个星系那么大),我们知道这个灯泡的尺度是 d,那么我们在地球上看这个灯泡的时候,灯泡会张开一个弧度
,我们知道,灯泡离我们越远,这个弧度会越小,近大远小嘛,于是根据几何关系 d/
.
也会给我们一个距离,这个叫角直径距离(Angular diameter distance)。
另外呢,我们可以假设随着这个灯泡在一根巨大的尺子上摆放着,尺子 0 刻度在地球上,灯泡在尺子上某一个刻度处固定,因为宇宙膨胀,会导致尺子的尺度也跟着膨胀,但是灯泡和地球的距离也随着宇宙膨胀一起在增加,所以灯泡在尺子上永远还在某一个刻度上,这个刻度也代表一个距离,叫共动距离(comoving distance ),comoving 的意思就是除去跟宇宙一起共同膨胀运动而导致的距离之外的距离。
当然,我们也可以对比观测到的这个灯泡的光谱峰值波长,对比实验室里测定的这种灯泡的峰值波长,得出红移量,再根据哈勃定律算出距离,这个叫哈勃距离(naive Hubble distance)。
好了,罗列了这一堆距离的概念,我们再简化一点模型,宇宙里的物质分布全部是均匀且各项同性的,所以这下你可以放心得说光线走的是“直线”了,或者说我们知道了灯泡在天上的赤经赤纬了,那如果再利用上边这些这么多种方法测出距离来,是不是就能如题主所说可以得到这个灯泡相对于地球在宇宙中的位置了呢? no,
这些测出距离的方法,虽然都来自于对同一个灯泡的观测,甚至用的都是同一批光子,但如果在宇宙学尺度上,结果却大不一样,下边显示了这些根据“观测”而推算出来的距离在宇宙学尺度上是如何变化的。
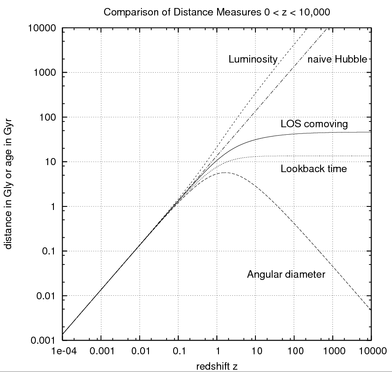
(wiki:distance measures (cosmology) )
这里的横轴就相当于在宇宙中的一个某一个确定的位置,也就是灯泡的位置。比如我测到了灯泡的峰值波长跟实验室波长相比,红移量 z=1,由此根据灯泡的视张角推出的距离和光度距离却可以差到 4 倍。这就纳闷了,同样都是这个灯泡,这两个对于距离的定义听起来也都没任何问题,为什么算出的距离会差这么多,到底哪一个距离才是更好的距离,是我想要的距离呢?答案是哪个都不是,因为在这种尺度上,测量本已经是个毫无意义的概念。
在邻近的时候,灯泡和地球之间的时空渐近平直(就像我们在地面上因为看到的距离太有限而觉得地球是平的),测量的定义才变得有意义,距离也蜕化为了欧氏几何的结果,从图上可以看到这些所有定义下的距离在低红移时候都蜕化为一个值。
而在远离的情况下,时空整体的弯曲开始表现出来,而由于光度距离(用到了球的表面积正比于半径平方)、角直径距离(用到了直角三角形里的三角函数)和哈勃距离这三个定义都跟一些几何原理是息息相关的,自然会受到影响,时空的弯曲对这些欧氏几何里的原理产生不同程度的修正,所以这些距离给出了不同的值,但是并没有哪个比其他的更有道理。
于是乎,题主提的这个“确立宇宙中的空间位置”这个提法,哪怕在最简单的假设下,哪怕有了最丰富的观测也是做不到的,因为这在相对论的时空观里本来就是个毫无意义的提法。
当然,在实际的宇宙学研究中,我们还是可以在指明我们说的是哪一种距离的情况下用长度来描述遥远天体的距离的