为什么尺规不能三等分一个角？

啊，我小时候也曾为三等分角而磨秃无数支铅笔……故事最后再说，我先回答问题。

『三等分角』是古希腊三大尺规作图难题之一，具体表述为：用只用圆规与一把没有刻度的直尺，将任意给定角三等分。

比如，如果给定的是直角，那么下图就是一种三等分的办法（图片来自网络）：

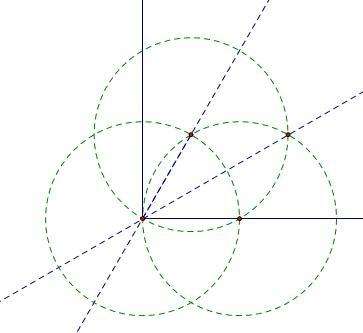
但可以看出，这个方法只对直角有效。

那么是否存在可以三等分任意角的方法呢？这个看起来并不复杂的问题困扰了数学家们两千多年，直到十九世纪才被证明是无解的。

接下来我试着解释一下为什么这是无解的。同样地，这只是小小的『科普』。为了可读性，我会牺牲一些严谨性。想要彻底理解，还是得看教材。

我先说一下证明的思路（采用引用格式以方便阅读）：

假设存在三等分任意角的方法。

由于我们可以用尺规作出 60° 角，那么我们就可以通过三等分 60° 角而作出 20° 角。

如果作出了 20° 角，那么我们就可以作出长度为 cos 20° 的线段。

然而，尺规无法作出长度为 cos 20° 的线段，所以不存在三等分任意角的方法。

就是这样。

我们一步步看：作 60° 角很简单，作一个正三角形即可，如下图（图片来自网络）：

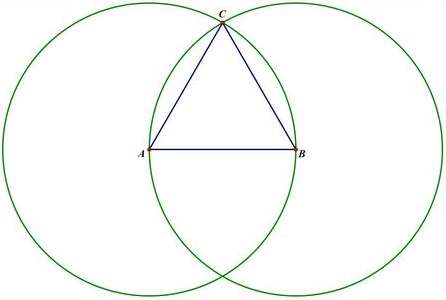
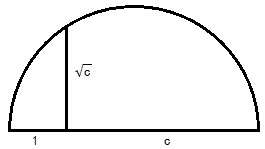
在有了 20°角的基础上，作出长度为 cos 20°的线段也很简单，只需要在一条边上与顶点距离为 1 的位置作另一条边的垂线段即可，如下图：

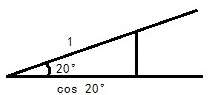
（如何过一点作垂线？这个不难，留作练习）

所以难点在于，如何证明『尺规无法作出长度为 cos 20° 的线段』。

（从解析几何的角度来看，『可以作出(c, 0)点』与『可以作出一条长度为|c|的线段』是等价的，所以我接下来可能会交替使用这两种表述。）

为什么作不出来呢？

因为尺规作图只能作出有理数域  上次数为 2 的幂的数，而 cos 20° 在  上的次数为 3。

说人话！！！

好吧好吧，我会解释的。在这之前，我们不妨先把问题反过来问：尺规作图能作出什么来呢？

基本的操作如下：

1. 过给定两点作直线；

2. 在给定点以给定半径作圆；

3. 确定直线与直线的交点；

4. 确定直线与圆的交点；

5. 确定圆与圆的交点。

基本操作有这五种。注意到，当我们确定了原点、坐标轴与单位长度之后，所有新的点只能通过后三种操作的方式被确定。

由于我们可以过一点作垂线，所以平面上所有的整点（即横坐标与纵坐标都是整数）都是可构作的；也就是说，我们可以作出所有的整数。

此外，尺规可以作加、减、乘、除以及开平方根这五种操作。

加、减是很显然的；乘法可以通过相似三角形来完成，如下图：

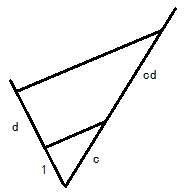
除法类似；开平方根同样是通过相似三角形来完成：

所以，既然整数都是可构作的，又可以加减乘除，那么所有的有理数都是可构作的。

而『开平方根』这个操作略特殊，为了更好地解释，我们需要引进一个新的概念：

域。

域的定义很冗长，不严谨地概括一下的话，域就是一个对加、减、乘、除都封闭的集合。

什么意思呢？就是说，对于一个域中的数字，无论你怎么用加减乘除去蹂躏它们，它们依然还是在这个域里。

举个例子，所有的有理数构成了有理数域 ，因为任意两个有理数做加减乘除之后依然是有理数。

除此之外常见的域还有实数域 、复数域  等等。

而整数集合  就不是域，因为一个整数除以另一个整数，得到的商不一定是整数。

有了『域』这个概念之后，我们再来看尺规作图：由于我们已经知道所有的有理数都是可构作的，所以如果我们只做加减乘除操作，我们还是只能得到有理数，还是在有理数域  内。

而『开平方根』这个操作就不一样了——它可以让我们离开有理数域. 比如我们对 2 开平方根，可以得到 ，而  就不属于有理数域 。

当我们在  的基础上多了  之后，我们可以通过加减乘除得到所有形如  的数（ 在  内，即为有理数）。

可以验证，所有形如  的数构成了一个新的域。这个域是包含  和  的最小的域，我们记作 。

所以，『对 2 开平方根』的操作的本质是『域的扩张』——把  扩张为 。

这个操作可以继续下去——对  中的 3 开平方根，得到  ，而  不在  内。于是，通过通过加减乘除，就可以得到包含  和  的最小的域，记作 。

我们把这样的『新加入了一个数而得到的扩张』叫作『单扩张』。

当然，我们可以通过同时向  中加  和  ，得到包含它们的最小的域  。显然， 与  是相等的。

但是，并不是每一次开平方根都会让我们得到更大的数域，比如对 9 开平方根，得到 3，而 3 仍然属于 。所以 。

为了衡量扩张的大小，我们引进『扩张的维数』这个概念。

学过线性代数的同学对此一定不陌生，『维数』就是一组基的大小。对于没学过线代的同学，我来稍微解释一下：

 到  的扩张是二维的，为什么呢？

因为我们可以从  中取出两个数，使得  中的每一个数都可以被唯一表示成  的形式，其中  在  内。

我们把这个维数记作 。

那么  直接到  的扩张是几维的呢？四维，即  。为什么呢？

因为我们可以从  中取出四个数 ，使得  中的每一个数都可以被唯一表示成  的形式，其中  在  内。

同样地， ，为什么呢？

因为我们可以从  中取出两个数  ，使得  中的每一个数都可以被唯一表示成  的形式，其中  在  内。

注意，这时  在  内而不是在  内，因为我们是从  扩张到  的！

由于  ，我们可以验证一下：

从这个例子中，我们可以看出，维数是相乘的关系：『从域 A 扩张域 B 的维数』乘『从域 B 扩张域 C 的维数』等于『从域 A 扩张域 C 的维数』；也就是说，.

而由于  ，所以 。

与『维数』密不可分的概念是『次数』。

『维数』是对于『扩张』而言的，而『次数』是对于『新加入的数』而言的。什么意思呢？就是说，，那么  在  上的次数为 2。

我们使用『次数』这个词，是因为是上的多项式的根，而这个多项式的次数是 2；同时，  不是任何  上次数小于 2 的多项式的根。

 叫作  在  上的『极小多项式』。

同样地，原本的域中每一个数的次数都是 1。

我们可以证明，对于单扩张来说，扩张的维数等于新加入的数的次数。

好了！关于维数和次数，需要知道的就是这么多！接下来让我们回到尺规作图！

之前说过，我们得到新的点的方式只有三种：直线与直线的交点、直线与圆的交点、圆与圆的交点。新得到的点，有可能在已有的域当中（维数与次数均为 1），也有可能在已有的域之外（维数与次数均大于 1）。

高中学的解析几何告诉我们，圆的一般方程是 ，直线的一般方程是 ；而求交点的坐标就是把两个方程联立起来，此时得到了一个一元二次方程。

而一元二次方程的求根公式是 ；于是，交点相当于是往原本的域当中加了  这个数。

根据之前的讨论，如果  在原来的域内，那么这就是一个一维扩张；如果  不在原来的域内，那么这就是一个二维扩张（因为  一定在原来的域内）。

也就是说，每次得到新的交点，我们都是在之前的域的基础上做了一维或者二维的扩张。

又因为扩张的维数可以相乘，那么每一次扩张出的域对于最初的域来说，维数都是 2 的幂。

对于任意可构作的数  来说，我们既然在有限步数  之内得到了它，那么  一定是在  与  之间。

由于  是 2 的幂，所以  一定是 2 的幂，所以  的次数一定是 2 的幂。

也就是说，我们所有能构作出的数在上的次数一定是 2 的幂。

那么 cos 20° 在  上的次数是多少呢？

由于 ；当  时，。

所以，cos 20°是方程  即  的解，而  是  上的不可约多项式（即不能被分解为次数更小的多项式的乘积），所以  是 cos 20° 的极小多项式，所以 cos 20° 在  上的次数是 3，不是 2 的幂。

所以尺规作图是作不出 cos 20°的。

所以我们没法三等分 60°角。

所以尺规三等分任意角是无解的。

证毕。

补充说明：

评论里有不少人问『长度为 1』的线段怎么作出来。

可能是我没有表述清楚，所以在此补充一下：

长度为 1 的线段不是『作』出来的，而是最开始『规定』的。

只有确定了『原点』、『坐标轴』和『单位长度』之后，我们才能确定一个坐标系。

所以，尺规作图的最开始，没有任何点参照，我们可以任意取一个点作为原点，接着以该点为圆心，任选一个半径画圆，并把这个半径的长度规定为单位长度『1』。

而当单位长度已经规定好之后，我们就不能『任意取点』或者『任意选半径』了，否则我们就不知道该点或该半径在已建立好的坐标系中的位置或长度，那么这个任意的选择就没有意义了。

以下是一些题外话

除了『三等分角』外，另外两道题是『倍立方体』，即用尺规作出体积两倍于给定立方体的立方体，和『化圆为方』，即用尺规作出与给定圆面积相等的正方形。

这两道题也都是无解的。

『倍立方体』问题等价于作出 ，而  是  上的不可约多项式，所以的次数为 3，不是 2 的幂。所以『倍立方体』是无解的。

哇！秒杀哎！

嗯，确实秒杀。我们现在对『三等分角』与『倍立方体』不可解性的证明属于『伽罗瓦理论』的领域（虽然不是核心领域）。1830 年，该理论由法国数学家伽罗瓦于18 岁（！！！）创立。

不过这两个问题的正式证明是由法国数学家汪策尔于 1837 年给出的，因为伽罗瓦创立这个理论是为了解决『五次方程不存在根式解』的问题……而且伽罗瓦在 1832 年就死了。20 岁。死于决斗。

『化圆为方』呢？

『化圆为方』问题等价于作出  ，而  （和  ）甚至都不是  上任何多项式的根，所以『化圆为方』是无解的。

哇！秒杀哎！不过为什么不是上任何多项式的根？

这有点麻烦，也是光用伽罗瓦理论还不够的原因。

 的超越性是德国数学家林德曼于 1882 年证明的。到此为止，困扰数学家们两千多年的古希腊三大尺规作图难题都有了答案。

当然，这三大难题依然困扰着今天的民科们。

以下是故事时间：

正如我在最开始所说的，我小时候也曾为三等分角而磨秃无数支铅笔……

大概是小学三年级的时候，我读了一本数学科普书：《特别要命的数学》（我超喜欢这本！！！）。

这本书中有一个章节叫《如何能流芳百世》：

首先先介绍了一些尺规作图的简单问题，比如作等边三角形、作正方形等等，最后是平分任意角。

接着，就是流芳百世的方法——解决『三等分角』问题：

以及，『化圆为方』：

由于把任意角平分非常简单，而『三等分角』看起来与其差别不大，于是我随即就找来了铅笔、直尺、圆规和白纸，开始试着解决『三等分角』问题……

我记不得到底为此花了多长时间，但半个月肯定是有的，每天晚上就画呀画……最后自然是没能成功……不过也并非一无所获，至少我歪打正着作出了正五边形……

后来初中的数学课上讲到了尺规作图，对我来说就像见到了老朋友一样。初三有很长一段时间我的数学课都是在与朋友一起研究『锈规作图』与『尺圆作图』这两个尺规作图的推广问题中度过的。

现在，坐在十年前曾尝试三等分角的房间里，写下了这篇关于『三等分角不可解性』的回答，想想真是有些感慨。至少自己这十年还是学到了一点点东西的，虽然只是一点点。

看着手边的代数课本中伽罗瓦的名字——

流芳百世。