隔夜的脏水底部沉积物为什么会排列成细纹?
 王不绿,今天的风儿好喧嚣啊 (≖_≖)✧
王不绿,今天的风儿好喧嚣啊 (≖_≖)✧
同意 @Jacobi LIU 对浅水波作用的解释。基于线性理论,我说一点自己的理解。
首先,根据边界条件和初始条件来看,脚盆系统可以理解为 reflective lateral boundary 的海洋系统(波传到边界后被边界反弹回来)。然后因为将脚提出水面后是产生了类似海啸或者潮汐的长波(当然也有一定的流动,但是波动更占主导)。所以,最开始的时候,盆里的水并不是向一个方向流动的,整个系统初期发展不能简单地理解成河流系统。
其次,为什么是长波(浅水波),假象一下把比日本还大的脚从太平洋牌洗脚盆里提起来会造成一场怎么样的海啸,如下图。为什么要提到长波的概念,因为它对这个问题的分析非常关键。
其次,在现实世界 ,有一种海床沉积物形态,砂浪 (sand waves),和一种月球主导潮汐半日潮 (M2 tide)。它们波长的量级分别是 100--800m 和 700km。脚盆底的细纹和把脚提出水面产生的长波可能有类似的在波长量级上的差别。所以细纹的产生似乎可以看作是砂浪的发展。简单来讲,盆底的细纹的产生是由于水粒子的竖向循环 (vertical circulation),使盆底的沉积物从它自身的波谷 (trough) 向它自身的波峰 (crest) 发展。这种竖向循环是水粒子的圆周运动 (orbital motion) 对于脚盆地 (海床) 的扰动 (perturbation) 做出的反应。然后勒,对于细纹的发展有两个力:
a) 向上的剪切力,由摩擦产生,作用于沉积物表面,提供沉积物运动的动力
b) 向下的重力,限制细纹坡度不会太陡。具体循环如图所示。在边界上的情况比较复杂,但是在远离边界的地方原理大致相同。脚盆里细纹之间有间隙只是说明你的脚还不够脏,题主下次一个月不洗脚再试试 xD 间隙可能会小一点。
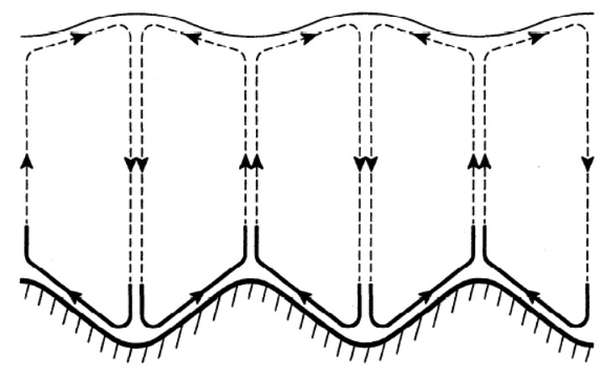
最后,如果抬脚越猛,你会发现最开始的时候细纹越尖,因为动力越足。但是由于阻尼 (damping) 的影响,波会衰减,再加上重力作用,细纹的高度又会降低一点。当波完全衰减后,似乎还有一些轻微的水体的流动继续影响细纹……吧?至于为什么把脚提起来产生的波其乱无比,但是最后产生的细纹却相对规律,这个我猜想是圆形边界的作用。具体圆形边界怎么反射波,我也不太清楚……Orz
总结:原因是水粒子受波动影响做圆周运动,条件是沉积物扰动,结果是竖向循环然后细纹产生。
如果不能理解水粒子在波的作用下的运动状态,请看下图(长波的情况是最下面图)。也可以看看视频感受一下,视频前面就是讲水粒子的运动方式。
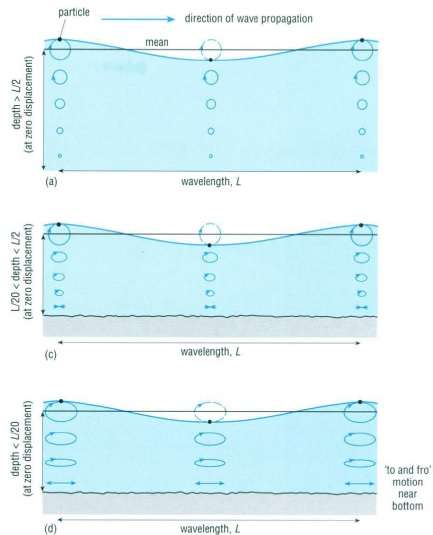
最后附上一张北海局部海床上的观测出来的 sand waves,是不是和脚盆底很像?
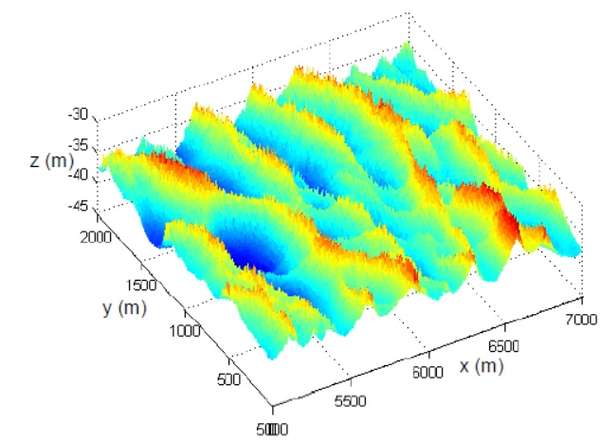
大概细纹的形成就是这样。如果表达有误,请斧正。
参考文献:
1. Brown, J., A. Colling, D. Park, J. Phillips, D. Rothery, andJ. Wright. 1989. Waves, Tides and Shallow-Water Processes. Pergamon Press, New York.
2. Hulscher, S.J.M.H., 1996. Tidal-induced large-scale regular bed form patterns in a three-
dimensional shallow water model. Journal of Geophysical Research C9(101), 20727-20744
--
谢谢大家喜欢这篇回答 :)
答案有微调,之后不会再变动,以及换了个更合适的视频链接。
感谢 @xsank mar 的指正。回答中,对水粒子的运动轨迹的描述应为 环形 而不是 圆周。
关于 @没有姓也没有名 不稳定扰动产生细纹的问题,在这里回答一下,因为篇幅稍大,见谅。
细纹是由扰动产生的(没有扰动就没有竖向循环),具体点就是最先假设是平坦的海床,再给上一个随机的扰动,比如随机波长或者振幅。我不确定沉积物的最后形态和最初的扰动有没有关系。目前的研究局限在平坦的海床对扰动的最初反应,只是最初的那一瞬间的发展趋势,比如趋向于哪个波数 k,增长率 (growth rate) 等。而对于影响沉积物平衡态 (equilibrium) 的机制还不清楚。所以沉积物最后的形态可能和最初扰动有关,也可能没有。
带有强烈误导性质的“稳定”和“不稳定”只是坑爹科学家的一种定义。他们认为任何扰动最开始的发展趋势是向平坦的海床进行就是稳定,也就是求解出来的波数 k 超级小(波长无限大),反之定义为不稳定 (╯‵□′)╯︵┴─┴。举个例子,这种坑爹定义同样出现在河流的两个分支 (bifurcations) 的研究里。他们定义在平衡态时,稳定就是两个分支都是通的,不稳定就是一个分支淤塞,另一个是通的。他们就爱这么玩概念╮(-_-)╭ 。