人为什么厌恶风险？

但是如果当事人充分的理性，应该去追逐利益的最大化：风险只是收益的不确定性，当投资时间足够长，最后的收益收敛于期望收益。

这是题主的困惑所在，我觉着这个问题的答案不仅仅在于“人为什么厌恶风险”，而是在于，人性为什么“不耐”。

故事是这样的，假设有两种投资的收益路径：

1. 每期收到 1 单位回报
2. 第一期收到 0.5，第二期收到 1.5，第三期收到 0.5，第四期收到 1.5........

注意在这两个投资里面，都没有不确定性。那么请问，你应该选择哪一种呢？

我想任何一个学过经济学的都会写出如下的效用函数（收益为  ）： 

这里面出现了一个  ，一个  。现在我们来看，如果 u 假设是一个 concave 的函数，那么一般来说我们认为这个人是风险厌恶的（有文献指出这里的 u 跟风险偏好系数并不等价，特注）。但是，如果我们假设 u 是一个 linear 的函数，也就是说是一个风险中性的效用函数，那么投资者会选择什么呢？

仍然是 1。为什么呢？稍微计算一下可以知道，如果假设 linear 的效用函数 u，第一种投资的收益路径计算出的效用为  ，而第二种投资的收益路径计算出的效用为  

那么问题来了，这两个谁大谁小呢？这要从  的涵义入手。这个  度量了“人性不耐”，明天的 1 块钱，只相当于今天的  块钱，如果人性不耐，那么明显  。如果  成立，那么通过简单的计算就可以得到，投资者会选择第一种。

更进一步，我们会发现，在一些简化的模型里面，  应该等于无风险收益率的倒数。

总结一下，我在这里没有假设所谓的“风险厌恶”，投资者仍然选择“风险小”的投资，可见在题主的这个疑惑里面，“风险厌恶”虽然有一定的解释能力，然而仅仅“人性不耐”就可以解决掉这个问题。

那么，现在我们反过来考虑，如果存在一个非常非常有耐心的人呢？我们现在考虑一个投资者准备投资 A 股。简单起见，我们假设这个投资者投资了 market portfolio，而 market portfolio 是简单的服从一个随机游走的：  ，  为 market portfolio 的价格，或者说是指数。同时，假设一个无风险收益率  ，其年化收益为 5%。

为了校准 market portfolio，我取出了从 2006-1-1 至今的上证指数，计算出  ，并使用以上的参数进行模拟。注意无风险收益率每天的收益约为 1.626e-5，也就是说投资股票从长期来看是有正的收益的，对应题主的“收益收敛于期望收益”，这里投资股票的收益长期来看是大于无风险资产的收益的。（这个计算，当然，不靠谱，因为相当于粗暴比较了 06 年的上证指数和现在的上证指数。不过仅仅作为一个近似的 calibration，此处不予较真）。

现在我们做一个实验，如果一个人随机一个时间点入市，他足够有耐心，一直持有这个 market portfolio，那么他手上证券的价格走势可能是这样的（蓝线表示一直持有 5%的无风险收益证券）：

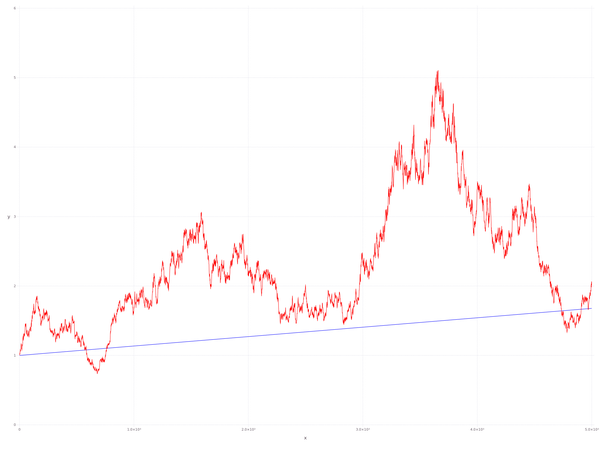
看起来运气不错，有一段时间几乎翻了 5 倍。不过也有可能是这样的：

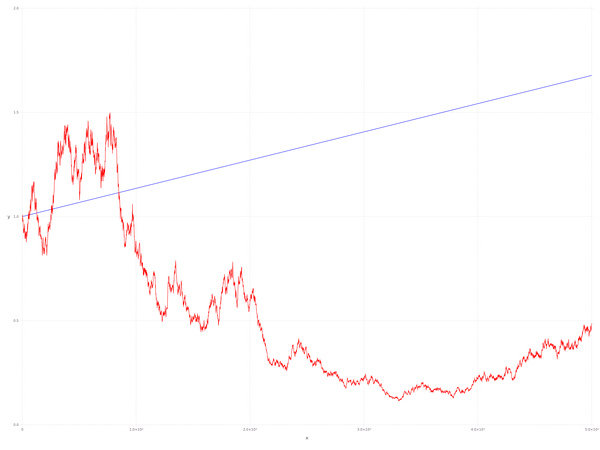
这也许就是 07 年的那些接盘侠吧。

现在我们考虑这个投资者，不仅非常耐心，而且非常有决断力：只要投资股票的收益大于等于无风险收益的两倍，那么就退出市场。请问他要等多久？

有了以上的参数的校准，我们可以做一些模拟，把以上的投资过程模拟 10000 次。同时，考虑到人的生命有限，模拟到 50 年（18250 天）即终止。code 之后附上，我们来看一下结果：

1. 为了获得超过无风险收益两倍的收益，平均需要 1821.72 天，也就是大约 5 年
2. 以上天数的标准差为 1982.18 天
3. 最少需要 75 天
4. 最多？50 年，也就是到了我们的上限
5. 50 年仍然没有达到这个收益率的有 8/10000 个

或者，我们来看一下直方图，注意横坐标为天数，5.0*10e3 对应着 13.7 年：

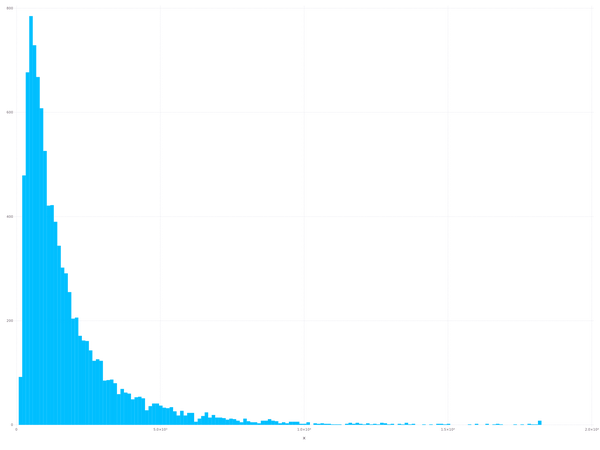
5 年的时间平均下来 10%的收益，你觉着怎么样呢？妥妥的跑赢了无风险收益率哇！以上的结果表明，如果你非常非常有耐心，跑赢无风险收益率几乎是肯定的。而且，如果你足够聪明，不在 2007 年那么高的点位入市，跑赢无风险收益 2 倍也不是很难的事情，最多 10 年左右的时间足够了。但是，请问有多少人会愿意采取以上的策略呢？

这里，就如同题主所说的，随着时间变长，投资的收益率不会有那么大的不确定性，而且预期收益更高，然而，绝大多数人仍然不会选择这样的投资策略。这也许就是所谓的“人性不耐”吧，谁会愿意等那么久呢？

附代码：