日报标题：咦，为什么几根棉签放在盒子里，会自动组成这种形状？
知乎用户，凭虚御风，不知所止。
这个东西叫做单叶双曲面：
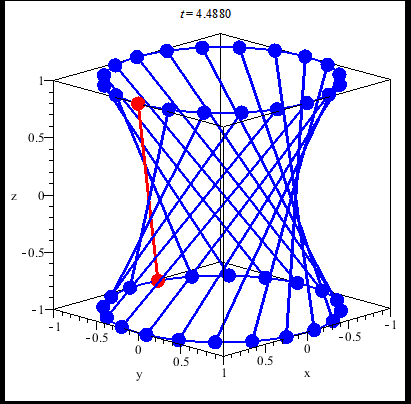
（图片来源：Hyperboloid）
其实这个方程是能推导出来的。题主问的是为什么会形成这个形状，那么我们就来归纳一下棉签到底处于什么样的条件。
首先对于单根的棉签而言，不难理解受到重力作用下滑，最终两端都在棉签桶的壁上。而对于多根棉签而言，由于他们的粗细和长度都相同，因此这里存在了两个约束条件：
1. 它们顶点和底端都在一个圆上。
2. 紧邻的两根棉签距离相同（也就是这个圆上的圆心角差距相同）。
接下来是粗糙的数学推导：
随便找一根棉签，假设它上下的坐标分别是：
（cosA, sinA, 1）和（cosB, sinB, -1）
这里假设了这个圆半径是 1，棉签自然垂落的高度是 2。具体数字并不影响最终形式，只是为了方便推导。
那么紧跟着它的一根棉签，旋转了一个小角度 x，上下坐标就应该是：
（cos（A+x）, sin（A+x）, 1）和（cos（B+x）, sin（B+x）, -1）
那么：
1. 两点可以确定一条直线。
2. 这条直线对于任意 x 成立，确定一条面。
于是我没事干推导了一下……
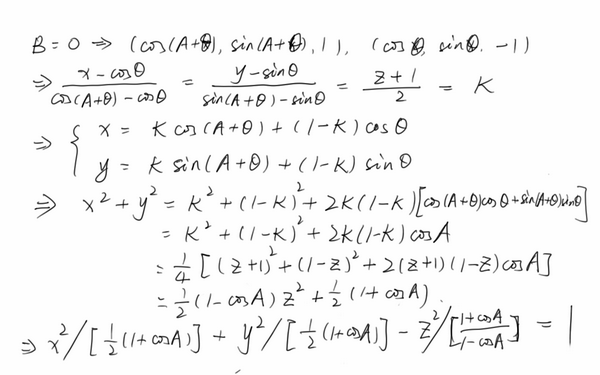
假设 B 等于 0，就是选一个特殊的起始点咯，然后第一个推导是两点的直线方程。后面暂时用 K 代替简化计算。
第二个推导就是把 x 和 y 分别弄出来。
第三个推导就是暴力运算了。
第四个推导只是把形式变得好看，类似于下面这个：
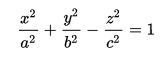
也就是单叶双曲面的方程。