日报标题:说起来,人类还真是不理性的动物啊
 胖子邓,活着,爱着,写着。
胖子邓,活着,爱着,写着。
来写一个科普向的综述好了。
「人在不理性时会如何决策」,这是行为经济学和实验经济学研究的基本课题。我们从一些显而易见的和“理性”似乎违背的事实出发,并给出行为经济学的解释。
在经典经济学中,理性就是效用形式在满足一些前提下对效用的最大化。
这些前提其中的一些是:

选不选择期望收益高的项目,并不意味着理不理性。因为期望收益高,也承担了更大的风险,因此单看收益不看风险偏好,不足以说明一个人理性还是不理性。但是在两种情形下出现了相反的评价,则必有一种选择不理性。
至于在博弈论中,理性虽然仍然是最大化效用,但谈理性必须基于信念体系,因此有很多种理性,序贯理性,理性,无穷阶理性,N 阶理性,贝叶斯信念下的理性等等等等。
而说到「人在不理性时会如何决策」,我们一般假定这里的理性指的是无穷阶序贯理性,因此理性,N 阶理性这些都可以看做是“不理性”。这一点实在难以科普,诸位凑合看吧。
另外,以下“悖论”“问题”均为实验平均而言。并不代表所有人都会这样选择。
以下是答案。
【1】 阿莱斯悖论:我们真的厌恶风险吗?
首先,在以下两种计划 P1,P2 中选择你最爱的方案:
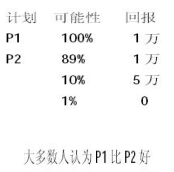
其次,在以下两种计划 P3,P4 中选择你最爱的方案:
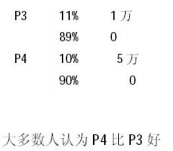
但实际上 P1+P4 = P2+P3!,也就是说如果我们认为 P1>P2,那么应该认为 P3>P4 才对!
一种解释——反射效应:对损失性预期的偏好是对收益性预期偏好的镜像
–收益方面:偏好确定性的收益
–损失方面:厌恶确定性的损失
也就是说我们对风险态度是不一致的(这也就可以解释为什么平时风险厌恶的人也会买彩票)
另一种解释是——Kahneman–Tversky 权重函数
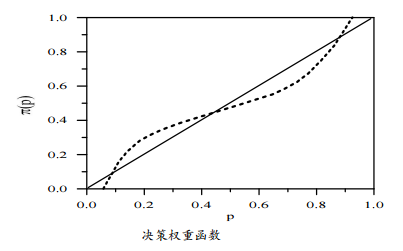 如上图所示,我们真正使用的是主观概率π(p)而非 p 来计算期望效用的,这种主观概率的特点是:低概率高估,高概率低估。极低概率为 0,极高概率为 1 。
如上图所示,我们真正使用的是主观概率π(p)而非 p 来计算期望效用的,这种主观概率的特点是:低概率高估,高概率低估。极低概率为 0,极高概率为 1 。
【2】偏好逆转(Preference Reversal)现象:我们的偏好固定吗?
- 比较两种方案
• A 28/36 的机会赢得 10 美元
• B 3/36 的机会赢得 100 美元
- 问题 1:若你可以在两种机会中选择一种, 你会选择哪一种方案?
大多数人会选择 A。
- 比较两种方案
• A 28/36 的机会赢得 10 美元
• B 3/36 的机会赢得 100 美元
- 问题 2:让你出售两种方案,你对哪一种方案的定价更高一些?
大多数人会给 B 的定价更高。
卡尼曼通过实验证明,人们的偏好并不存在一个一致的顺序。
人们在 A、B 两 事物中任选其一时,他若选择 A,但在让他转让这两事物时,他却倾向于 B 的价格比 A 更高。
一种解释——展望理论的值函数
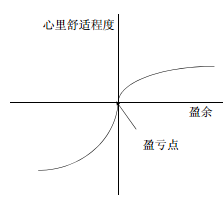
如上图所示,在零点上下,对于风险的评判是不一样的。(这可以看做是反射效应的进一步拓展)
也正是基于此,如果有两个消息需要告诉对方,怎么表述能让对方感到效用最大?
↓↓↓↓↓↓
- 都得益,分开表述。
- 都损失,一起表述。
- 大得益与小损失,一起表述。
- 大损失与小得益,分开表述。
【3】 为什么五块钱掉了不心疼,五块钱的甜筒掉了会心疼?
情形 A:你已经花 100 元买了一张音乐会的门票, 到达音乐厅时,你发现门票丢了。售票处还在以同样的价格卖票,你会不会再买一张票?
情形 B:你预订了一张 100 元的门票,到场取票, 到达音乐厅后,你发现丢了 100 元,假设你还有 足够的钱,你会不会按原定价格买票?
一种解释——心理账户(mental accounting)
一个账户为音乐会账户,另一账户为现金帐户,当丢了门票时,你会认为再买门票花费 200 元。
【4】疫情村(Tversky and Kahneman , 1981):某个村子有 600 人,正在遭遇疫情的威胁,营救 方有两个营救方案。
• 方案 1:200 人获救
• 方案 2:600 人获救的概率为 1/3,没人获救的概率为 2/3
实验结果:选择方案的人数比例为方案 1:方案 2=109:43
• 方案 1:400 人死亡
• 方案 2:600 人获救的概率为 1/3,没人获救的概率为 2/3
实验结果:选择方案的人数比例为方案 1:方案 2=34:121
一种解释——孤立效应:从事物的不同侧面,可能导致不同的偏好
【5】 哈根达斯冰淇淋
现在有两杯哈根达斯冰淇淋, 一杯冰淇淋 A 有 7 盎 司,装在 5 盎司的杯子里面,看上去快要溢出来 了;另一杯冰淇淋 B 是 8 盎司,但是装在了 10 盎司 的杯子里,所以看上去还没装满。你愿意为哪一 份冰淇淋付更多的钱呢?
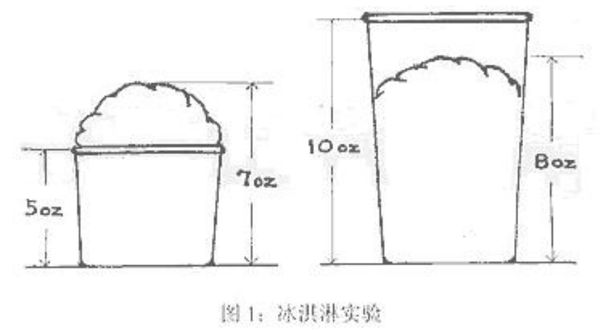
实验表明:平均来讲,人们愿意花 2.26 美元买 7 盎司的冰淇淋,却只愿意用 1.66 美元买 8 盎司的 冰淇淋。(这也可以解释为什么肯德基用小袋装超满薯条而 不是用大袋较满薯条)
【6】博弈论中的“非理性”
当然博弈论里也零星地有提出很多对理性挑战的博弈,因为很杂,就随便讲几个了。(而且其实博弈论中对理性的要求本来就存在很多不一样的定义,因此也不太好说是“非理性”)
【6.1】 Jerry 已经提到的最后通牒博弈
两参与人 A,B,A 报价 x,如果 B 接受报价,那么 A 获得 x,B 获得 10-x,如果 B 不接受报价,两人都不获得收益。
理论上讲,只要 A 的报价小于 10,B 都会接受。然而在实际中并非如此,大部分人会认为 A 过于“贪心”而拒绝掉 A 的高价 。
【6.2】 蜈蚣博弈
这个博弈相当有趣:两个参与者按如下形式游戏,看上去如果一直合作下去会有(100,100)的收益。
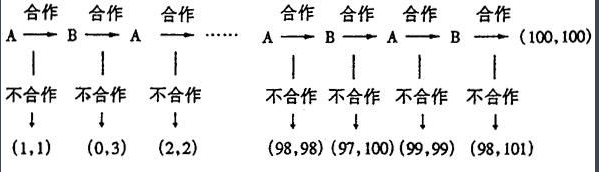
然而这个博弈的序贯均衡竟然是在第一期就结束!
我们从最后一期看起:如果到达最后一期,B 不合作反而会得到 101,因此 B 其实不会合作;
而 A 知道 B 在最后一期不会合作,A 就只能获得 98,因此他会选择在倒数第二期就不合作,两人获得(99,99)
可 B 意识到 A 这样选择,他会在倒数第三期选择不合作,获得 100;
这样依此类推,他们竟然只能获得 1 的收益。试想,如果两人能撑两期,都能分别获得(2,2)的收益!
而在实验中,确实大部分人都会玩 4 期以上,这和序贯理性是有所违背的。
当然,最有趣的一点是:在蜈蚣博弈的实验中,经济学家曾让一些围棋高手作为被试,结果他们的结果则是几乎完全符合理性:他们全部在第一次或第二次就结束了博弈。
【6.3】囚徒困境的有限重复和无限重复博弈
囚徒困境是大家都熟知的博弈。
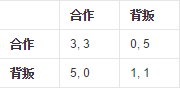
纳什均衡解是在(背叛,背叛)
但如果我们让这个博弈进行很多次,大家多次交手,是否会选择合作,信任对方?
如果进行无限次重复,可以证明,最优的决策是信任对方。
但如果进行有限次,无论有限值有多么大,根据【5.2】中类似的逆向归纳,我们都可以知道,在最后一期,人们是会选择背叛的,因此依此类推,在每一期都会背叛。
然而在实验中,大部分人即使在有限次博弈中仍然选择信任。
对【6.2】【6.3】的解释——囚徒困境有限重复和蜈蚣博弈本质的问题都在于,序贯理性对理性的要求其实是很高的。
后来有人提出了理性,简单来讲就是说,我们的理性容忍期望效用有
的偏离,如果这种偏离是有可能获得收益的。

![[LoliHouse] Princess-Session Orchestra - 15 [WebRip 1080p HEVC-10bit...](http://s2.loli.net/2025/04/09/QO618K72ytGZmDJ.webp)















