日报标题:一滴污水就能让清水变浊,但一滴清水却不能让污水变通透
 曾加,把诗意的理性献给你 / 公众号PlusZeng
曾加,把诗意的理性献给你 / 公众号PlusZeng
这是一个很棒的问题,忍不住来回答,抛砖引玉一下。
题主的真实含义是:
一杯清水中,滴入一滴污水,(很明显地)变污浊了,但一杯污水中,滴入一滴清水,却没有(明显)变清澈(肉眼很难察觉),原理是什么?
由此看来,现有的大部分答案都很难令人满意。
现有的回答主要分为三类:
- 纠结于·“清”和“浊”的定义,认为“浊”的定义比“清”宽泛得多,有一点点“脏”的水就是浑浊的。
——这话虽然不错,但似乎曲解了题主的题意(把题意窄化,将相对“清澈”理解为绝对“清澈”),有抖机灵之嫌;
- 用 “熵” 来回答,认为变浑浊是熵增的过程,是自发的,而反过来需要做功,是比较困难的。
——这话本身也不错,但我认为并不能解释这道题。因为 “熵” 和 “浑浊” 并非是直接联系,真正与 “熵” 对应的,是 “混乱”,这两个词是不一样的,比如,很多液体本身就是浑浊的,但也可以是纯净物,它并不“混乱” ;
- 用“量变”和“质变”来解释,清水是 0 ,浊水是 1 ,清水变浑是从无到有,是质变,而浊水变清是量变;
——在物理问题下这么答,好像有点鸡汤吧?
只有 @D Flip Flop 的回答道出了问题的一部分本质:
混合后是否浑浊是“或”运算
我赞同他的回答,只是他的回答太简略了,需要提供一个详细的解释。
【一】
首先我们得明白,什么是“污浊”?
我们觉得一个东西污浊,本质是因为它的透明度低,而透明度低,本质是光线穿过率低。
而光线穿过率低,是因为有分子阻碍了光线的前进。
“透明度” 其实是一个有点复杂的物理概念,要计算物质的透明度,我们得考虑不同分子的浓度、分子的大小、结构、密度、折射率等等,计算过程也非常复杂,用来回答这道题,显然是杀鸡用牛刀了。
所以,不妨 简化一下模型,像这样

假如我们要研究的分子,形成成立体点阵,铺满整个平面。
- 分子之间其实是有缝隙的,为了简化计算,先不管它;
- “清水”并不是完全透明的,但也假设是完全透明的吧;
- “浊水” 中的杂质并不是完全不透明的,但也假设是完全不透明的;
于是我们建立了一个简单的模型:
一共 1000 个点,代表 1000 个分子,可以是 “清水” 的分子,也可以 “杂质的分子”,这些分子,铺满了 10*10*10 的立体空间,每个大小都是 1*1*1 ,它们的中点坐标 (x,y,z) 从 (0,0,0) ~ (9,9,9) ;
考虑在 xy 平面上的 “透明度”,即垂直于该平面的 “光线”;
xy 平面,一共 100 个“位置”,从 (0,0)~ (9,9),
我们定义一个“位置” 是“透明的”,
当且仅当对于任意 {0,1,2……9},
都是透明的
(这是容易理解的,因为光在垂直于 xy 平面传播时,所遇到的 10 个点,只要有一个点不透光,这路光线就不会穿过来)
【二】
一开始,这 1000 个点都是透明的,所以 xy 平面的这 100 个位置也是透明的。
下面我们加 “杂质”,把部分点变得 “不透明”。
为了探究 xy 平面的不透明度,我们只要考虑“杂质” 在 xy 平面的投影即可:
当杂质是 1 个点时, 显然,xy 平面的 100 个位置,有一个位置变得 “不透明” 了,总的透明度变为了 0.99 ……
当杂质是 2 个点时,设两个点分别(x1,y1,z1)和(x2,y2,z2),则有两种可能:
- 若 (x1,y1) = (x2,y2),则两个杂质点投影到 xy 平面是同一个位置,所以透明度还是 0.99 ;
- 反之,两个杂质点投影到 xy 平面是不同位置,透明度为 0.98 ;
考虑到两种情况的不同概率,我们需要做一个加权平均,最后得出两个杂质点的 “平均透明度”,大约是 0.9801
类似地,我们可以计算当杂质点的个数为 n 个的时候,xy 平面的 “平均透明度”。
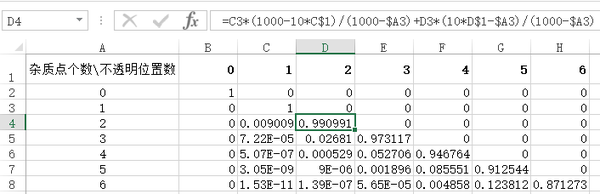
计算方法不是很容易,我用 动态规划 的方法,由于懒得写代码 ,
所以就直接在 Excel 中编程,像这样 (中间一块代表概率):
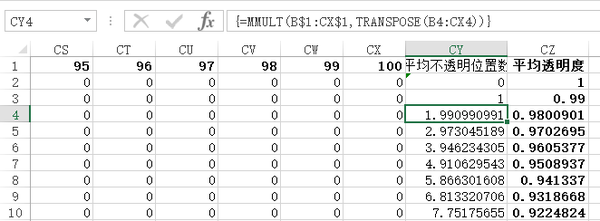
最后可以算出 平均透明度,像这样:
最后得到下面的图:
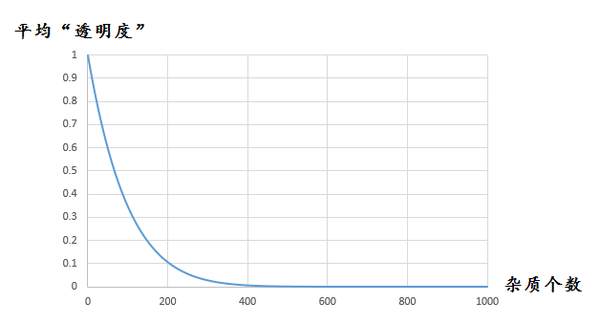
其中,横坐标为“杂质的个数”,纵坐标为 “透明度”
从图中我们可以看到,透明度曲线的“斜率”的绝对值,随着“杂质”的增多而降低,而且,几乎可以近似成等比例衰减函数。
OK,答案呼之欲出了。
假设总共有 1000 个分子,一滴水是 10 个分子。
A
- 在清水中加入一滴浊水,就好比在 1000 个透明分子里混入了 10 个不透明分子,即 1010 个分子中有 10 个不透明分子,等效于 1000 个分子中有 9.9 个不透明分子
透明度从 1 下降到了 0.905 —— 变化几乎达到了 0.1 ,很明显
B
- 在浊水中加入一滴清水,就好比在 1000 个分子中,可能本来已经有 100 个不透明分子,我们滴完清水后,变成 1010 个 分子中有 100 个不透明分子,约等效于 1000 个分子中有 99 个不透明分子——仅仅相当于减少了 1 个不透明分子
透明度从 0.347 上升到了 0.351 —— 变化是 0.004
由于不透明度越高,透明度曲线斜率的绝对值就越小,加上 B 中的“等效不透明分子”变化要小于 A ,那么——
就透明度而言,无论是绝对值的变化,还是从比例的变化,B 都要远远小于 A 。
这就从直观上解释了题主的疑问。
【三】
当然,真正的“透明度”计算模型,比这个要复杂得多,但大体原理是一样的。
“透明度曲线的‘斜率’的绝对值,随着‘杂质’比例的增高而降低” 这个结论,依然成立。
那么,为什么会算出这个结果呢?
回到这句话:
混合后是否浑浊是“或”运算
现在,它是不是容易理解一些了?
在一瓶清澈的水中,混入一点点 “浑浊” 分子,由于数量比较少,投影后很少会有空间位置的重合,所以几乎每一个都会遮挡我们的视线,使水的透明度下降;
正如这样的或运算:
- 原来:0 || 0 || 0 || 0 || 0 = 0
- 现在:0 || 0 || 0 || 1 || 0 = 1
(左边多了一个 1,右边从 0 变成 1 )
而一杯混浊的水中,混入一点点 “清澈” 分子,本质上,和一杯浑浊的水,去掉一点点浑浊分子是类似的。
只是,当浑浊分子的数量达到一定的量的时候,去掉一点点浑浊分子,在空间上看来,很多时候并不能增加透明度,因为在这条线上,可能还有别的分子遮挡了光线。
正如这样的或运算:
- 原来:0 || 1 || 1 || 1 || 0 = 1
- 现在:0 || 0 || 1 || 1 || 0 = 1
(左边少了一个 1 ,右边没有任何变化)
正因为这样的区别,才会有这样的结论:
原来的水越清,杂质浓度变化在视觉上的表现越明显。
你看,看起来很简单的生活现象,背后可是蕴含着不太简单的道理的。
扯淡的分割线
“一杯清水因滴入一滴污水而变污浊,一杯污水却不会因为一滴清水的存在而变清澈”
这句话,其实是一个绝妙的比喻。
比如,在工作中,
一个优秀的团队,往往会因为一个糟糕的人变坏。
一个糟糕的团队,却很少因为一个优秀的人变好。
为什么会这样?
因为,一个项目是否失败,往往是 “或” 运算。(牵一发而动全身)
人生的很多事情,不也是如此吗?
【转载请注明出处,商业转载请私信】