日报标题:看完这篇混凝土受力的原理,希望你对此再无疑惑
 猪小宝,博士僧 | 一级注册结构工程师
猪小宝,博士僧 | 一级注册结构工程师
跟我的其他专业知识方面的答案一样,如果您看完我的答案,还是不明白,欢迎您来亚特兰大抽我。
多图预警。
对于知乎上结构设计方面的问题,我是希望我能「遇一山平一山,见一寨拔一寨」,希望我答了之后大家看了再无疑惑。
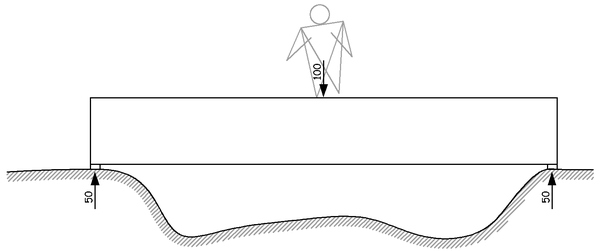
一根简支梁,跨度是截面高度的 8 倍。一个集中力作用在简支梁的中间,比如大小是 100, 那么根据我们在结构力学里学到的知识,很简单,两端的支座反力大小相同,分别为 50。两个向上的 50 加起来,跟中间这个向下的 100 平衡。
同样,根据结构力学的知识,我们也能知道,这根简支梁各个截面的剪力大小均为 50。只不过因为符号的定义,中点两侧的剪力一边是正 50 一边是负 50 而已,中点处剪力的突变对应外加的集中力。
只讨论剪力,不讨论弯矩的话,以上就是结构力学能告诉我们的所有内容。如果我们想知道梁的「抗剪机理」,或者说,这中间的 100 是怎么传递成两端的两个 50 的,整个梁的内部到底发生了什么,那么我们就要用到混凝土结构设计的知识了。
其实道理很简单,甚至都不需要很高深的材料力学知识,简单的结构力学知识就足够了。
为了方便起见,以下示意图中压力以蓝色表示,拉力以红色表示。
我们先从外加的竖向集中力开始,一个大小为 100 竖直向下的集中力作用于梁上表面的中点处,那么根据力的平衡,在这一点,一定还有合力大小为 100 竖直向上的一个或者一组力。否则,这一点的力的平衡就不能满足。
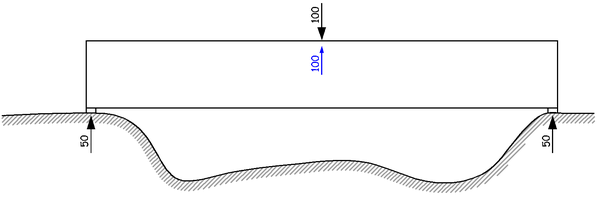
如果这也是一个竖直向上的集中力,大小为 100,混凝土承受的压力,那么可以不可以呢?至少在这一点看来,是可以的。
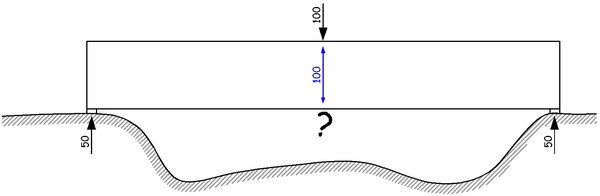
但是呢,这个压力继续向下传递,到达梁的底面,这里就出现问题了,因为底面外面就是空气,没有任何可以跟这个力平衡的可能。当然,你可以在这里加一个支座,用向上的支座反力来平衡,这样问题就解决了,但这样梁里面也没有剪力了,这梁也不是简支梁了,所以不在我们讨论之列。另一个解决方案是采用弯起钢筋,用斜向上的钢筋拉力平衡这个向下的力,但是随着人工费用的大幅上涨,弯起钢筋早已退出历史舞台,所以也不在我们讨论之列。
看,这条路算是走进了死胡同,我们只能推倒重来。
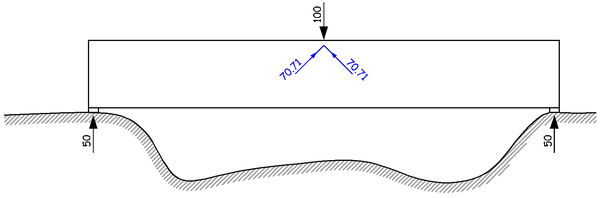
一个集中力不行,我们就换两个斜向的分力。外力竖直向下,大小为 100;内部的抵抗力可以是两个斜向 45 度的力,大小为 70.71,也就是 50 乘以根号 2。这样,这两个力的水平分力大小为 50,方向一个向左,一个向右,正好互相平衡;这两个力的竖向分力大小为 50,方向向上,加起来刚好和外力的 100 平衡。
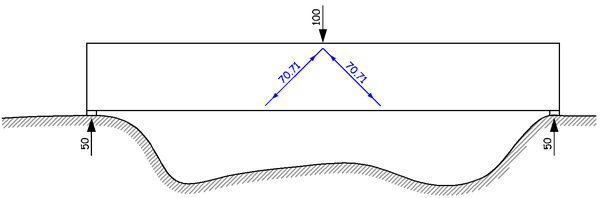
这两个斜向的力向下传递,到达梁的底面。这时候,我们就该动动脑筋,想想该怎么继续平衡这两个力了。
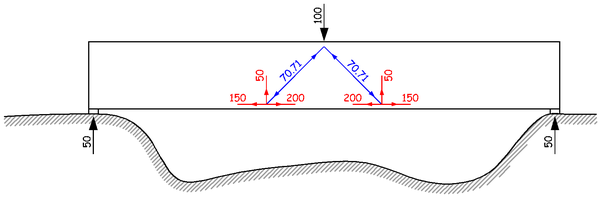
在底面处我们有什么?大声回答!对,我们有受拉的纵筋。所以,答案就来了。这两个 45 度斜向下的力,水平分力大小为 50,被节点两侧的纵筋拉力的差值平衡,也就是 200 减去 150 等于 50,刚好 50;这两个斜向下的力,竖直分力大小也为 50,被节点处竖直向上的箍筋拉力平衡,也就是说,这些箍筋需要提供大小为 50 的拉力。
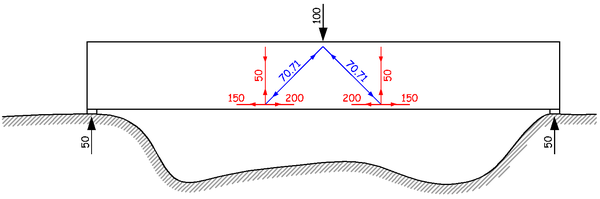
接下来,箍筋的 50 的拉力继续向上传递,到达梁的顶面。下面的问题,就是如何平衡这两个顶面处的拉力。
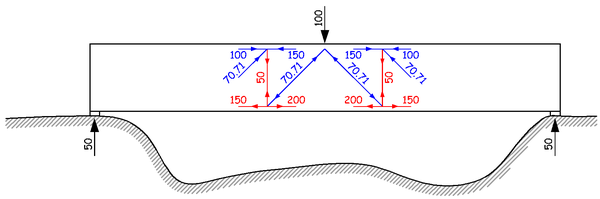
在顶面处我们有什么?大声回答!对,我们有混凝土受压区。这个竖直向下的 50 的力,竖直方向由斜向上的大小为 70.71 的力平衡。而这个斜向上的力同时也带来了水平方向的分力,所以水平方向要由两侧的混凝土受压区的压力的差值来平衡,也就是 150 减去 100 等于 70.71 的水平分力 50。
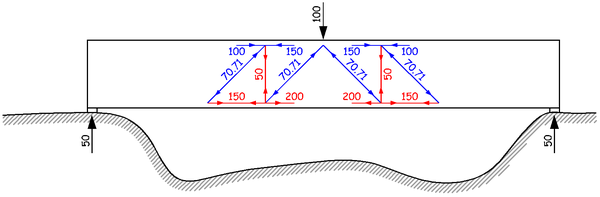
这个新增的斜向的大小为 70.71 的力,继续向下传递,与纵筋的拉力相交于梁底面。下一个问题,就是如何在梁底面这个位置平衡这个斜向下的力。
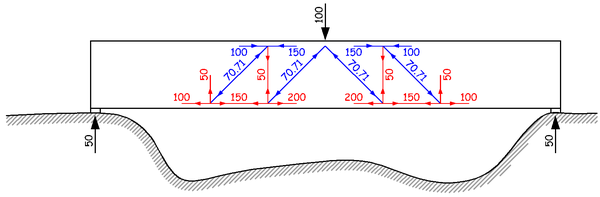
相信大家已经猜到了,很简单,回到第一步,再循环一遍。水平分力由纵筋的拉力差值平衡,竖直分力由箍筋的拉力平衡。
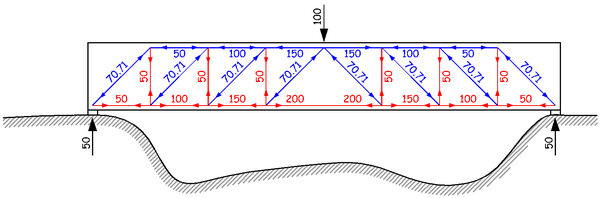
然后继续重复再重复,直到力传递到支座为止。当最终到达支座的时候,竖向分力不再需要箍筋,而是直接由竖直向上的支座反力平衡;水平分力则是直接被一侧的纵筋拉力平衡,因为另一侧已经到头了,没有纵筋了。
检查一遍全过程,取半结构,检验一下水平力、竖向力、弯矩平衡。竖向力,集中力向下 100,支座反力向上 50,蓝色斜向压力竖向分力 50,100 等于 50 加 50,没毛病;水平力,纵筋红色拉力 200,混凝土受压区压力 150,蓝色斜向压力水平分力 50,200 等于 150 加 50,没毛病;弯矩,对集中力作用点取矩,50 乘以梁的一半长度,200 乘以梁的高度,梁的一半长度是梁高的四倍,50 乘以 4 等于 200 乘以 1,没毛病。
回顾整个过程,中间施加的集中力,先是分成两半,分别斜向下,然后被箍筋拉回上面,然后再斜向下,然后再被拉上来……一直到支座为止。
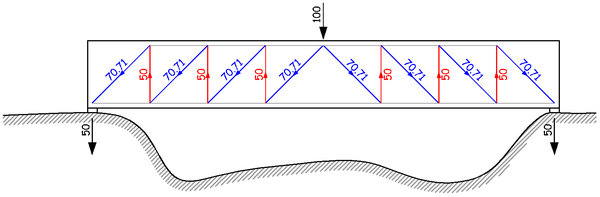
简单说,外力的施加可以看作注水口,支座反力可以看作出水口。注入 100 的水,分成两半,各自沿着蓝色的斜向管道流下去,然后被带有抽水功能的红色管道抽上来,然后再流下去,然后再抽上来……一直到达两端的出水口,每端 50,最终流入大地。
既然是一个连续的「力流」流动的管道,那么哪一个环节出问题都不行。蓝色的管道必须没问题,也就是说,混凝土必须足够结实,能够承受这个斜向下的压力;红色的管道必须没问题,也就是说,箍筋要足够结实,能够承受这个竖向向上的拉力;注水口和出水口也必须没问题,也就是说,集中力作用点和支座处的局部承压要足够,不能发生局部的承压破坏。
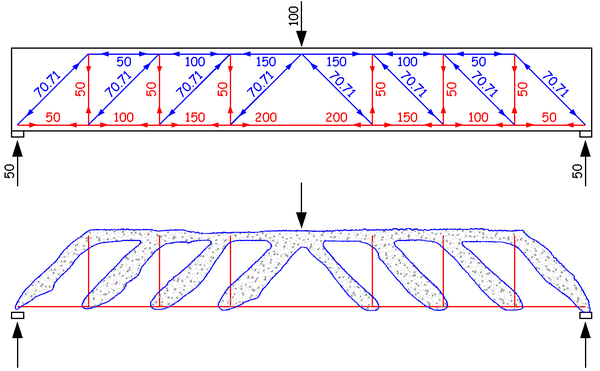
通过这样的分析,事实上,一根连续的混凝土梁变成了一个格构化了的桁架,受压杆件为混凝土,受拉杆件为纵筋和箍筋。仅就承受这个集中力导致的剪力而言,事实上,只有这些部分是发挥了作用的。在受力的分析上,跟木桁架、钢桁架没有本质的区别,只不过是一部分杆件是混凝土一部分是钢筋而已。
以上就是受力「分析」的过程,下面就要进入「设计」了。注意,之所以上面是分析,是因为上面所有的步骤都是抽象化了的、概念化了的东西,并不是真实的;而下面的设计,则是要把上面的理想化的分析体现到实际的现实中。上面的分析,只是告诉了我们力的流动,而下面的设计,则要给出最终的配筋方案,比如箍筋直径多少、间距多少等等。
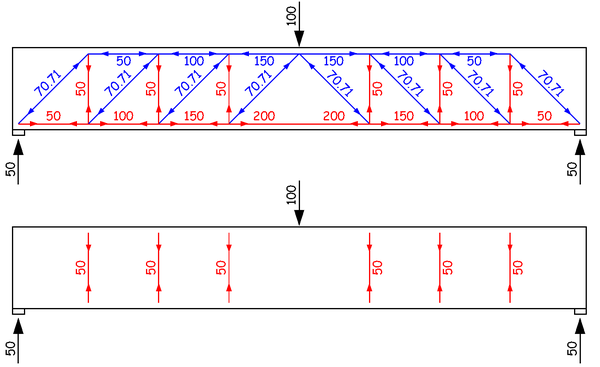
既然是讨论箍筋的设计,首先我们看一下在我们最终的分析结果里,跟箍筋有关的部分有哪些呢?其实就是这些竖向的红色拉力。也就是说,箍筋设计的目标,就是可以安全的承受这些竖向拉力,就像我们上面说的,在外力从作用点流动到支座的过程中,起到把力流从梁底面提升到梁顶面的作用。
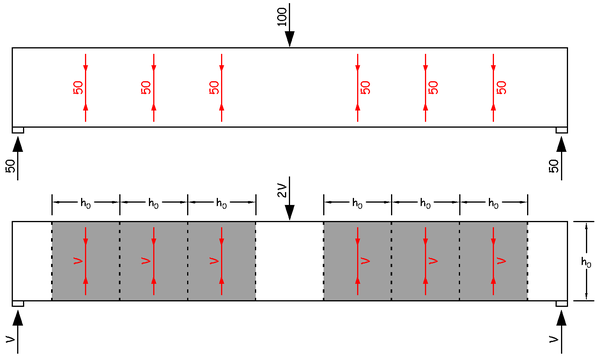
下面我们就要从抽象回到具象了。在我们的抽象化、理想化的分析模型里,因为是 45 度角,所以每个红色拉力之间的间距其实就是梁的高度 h0。也就是说,我们得到了一个结论,就像上图中阴影部分所示,虚线分割的每一个阴影部分内部的箍筋,都必须提供这个 50 的拉力。换句话说,集中力 2V,支座反力 V,截面的剪力其实就是 V。每一个长度为 h0 的阴影部分的箍筋加起来,必须提供大小等于 V 的拉力。
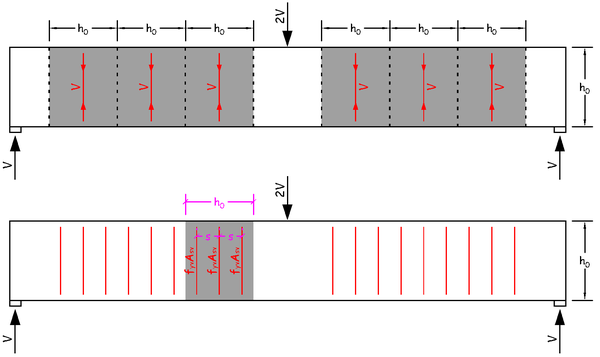
现在已经很明朗了。假设我每一排箍筋的面积是 Asv,箍筋的强度是 fyv,那么这每一排可以提供的拉力就是面积乘以强度,也就是 。每一个阴影部分的长度是 h0,相邻两排箍筋之间的间距是 s,那么这每一个阴影部分里面的箍筋排数就是长度除以间距,也就是
。
知道了单排箍筋的拉力,又知道了箍筋的排数,那么这每一个阴影部分里的箍筋的总拉力就是 。
而根据我们上面的分析,每一个阴影部分的箍筋总拉力,必须满足梁的剪力,也就是 V。
所以呢,
稍微变换一下形式,
好了,现在让我们打开混凝土结构设计规范,看看里面的公式:
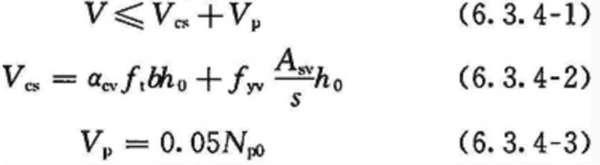
对比一下,明白了吗?
就是箍筋做出的贡献,依据就是我们上面的分析;
则是假设完全没有箍筋,一根纯混凝土梁的近似抗剪承载力。这两者加起来,就是一根钢筋混凝土梁最终的抗剪承载力。
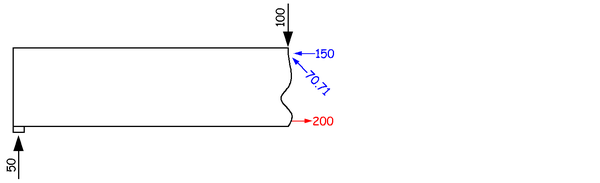
另一个相关的问题就是,如果我们这根简支梁非常短又非常高,也就是所谓的深梁,那这时候其实只需要斜向下的一个传递就够了,所以不需要额外的箍筋。
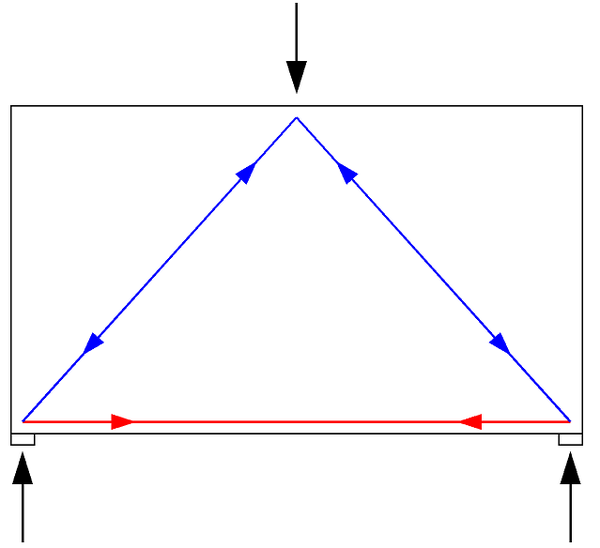
比如就像这样一根深梁,一次传递,外力就能流动到支座,所以就不需要中间的竖向传递的箍筋了。而深梁设计的核心问题也就是底部的纵筋要至少能平衡掉这个斜向压力的水平分力。
如果您对混凝土抗剪的受力机理或者桁架模型感兴趣,欢迎继续点击相关问答和专栏: